1 前言
建筑限界是邻近线路的建筑物或设备(与机车车辆相互作用的设备除外)不得侵入的最小横断面尺寸轮廓。列车运行在曲线上时,转向架中心点沿铁路中心运行,车辆本身不随着线路弯曲而弯曲,车体中心线与轨道中心线不吻合,车辆两端向曲线外侧偏移一个量(W外),而车辆中部向曲线内侧偏移一个量(W内1);由于曲线外轨设置超高,车辆向曲线内侧倾斜,使车辆限界的控制水平方向上移了一个量(W内2),
这是圆曲线限界加宽的计算依据[1]。
现行规章规定的建筑限界计算都是针对圆曲线范围和线路平面限界加宽,对于缓和曲线段平面如何计算没有详细规定,垂向加高及降低计算方法仅介绍站台部分,其他建筑物没有规定,这样难以检算特殊情况下的建筑限界,这个问题有必要进一步研究。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
2 曲线地段建筑限界常用计算方法
铁路建筑限界是一个闭合的包络轮廓线,由于受曲线平面及超高的影响,铁路建筑限界包络轮廓线对于线路中心,会发生平移和倾斜,曲线上的铁路建筑限界在横向必须加宽,在垂向必须加高或降低,故在曲线地段铁路建筑限界重分布,下面就这方面的规章规定进行分析。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
2.1 《铁路技术管理规程》[2]关于建筑限界的规定
铁路线路曲线限界加宽计算公式如下:󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$W_内=W_{内1}+W_{内2}=\frac{40500}{R}+\frac{H}{1500}\times h\quad(公式1)\\W_外=\frac{44500}{R}\quad(公式2)\\W=W_外+W_内\quad(公式3)$$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
\(\frac{40500}{R}\):车体中心与线路中心偏离值,转向架中心间距18m。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
\(\frac{H}{1500}\times h\):曲线超高引起车体倾斜的加宽,其中 H为计算点自轨面算起的高度,h为圆曲线超高值。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
\(\frac{44500}{R}\):车体端中心线偏离曲线中心,转向架间距18m,车体长度26m󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
根据以上公式可知,铁路曲线限界加宽主要是由内侧加宽和外侧加宽两部分组成:󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
一是内侧加宽:由车体中心线偏离线路曲线中心线产生的内侧加宽(mm)和因外轨超高引起车体向曲线内侧倾斜产生的内侧加宽两部分组成(公式1)󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
二是外侧加宽:车体中心线与线路曲线中心偏移产生的加宽(公式2)。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
2.2 《铁路车站及枢纽设计规范》[3]关于建筑限界的规定
第3.1.3条规定:“……位于曲线内侧的旅客站台,如线路有外轨超高时,应降低站台高度,降低的数值为0.6倍外轨超高度”,这是对站台垂向加高及降低进行的规定。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
综合以上现行规定的铁路建筑限界计算方法,对于缓和曲线段平面及垂向加高及降低如何计算,没有介绍,不同的列车车辆类型车辆长度与车辆转向架中心间距离也不同,以述公式不能直接计算。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
由于以上原因,现行规章规定的建筑限界计算难以适应复杂的限界判定,如跨线桥、矮柱信号机、信号箱、高低站台等设备及建筑物限界,现提出利用坐标平移旋转法绘制CAD图进,可较好地解决这个问题。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
3 绘制铁路曲线限界与建筑物位置关系图
根据建筑限界尺寸数据资料,建立坐标系并进行坐标平移与旋转,可精确绘制CAD铁路曲线限界图,判定建筑物侵限与否,其方法和步骤如下:󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
3.1 在铁路建筑限界轮廓线上建立直角坐标系
根据已知铁路建筑限界轮廓线至线路中心的距离与高度值,建立以曲线下股钢轨中心线为纵坐标轴,以曲线下股钢轨顶面水平线为横坐标轴建立初步坐标系,如图1。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

图1 直线地段铁路建筑限界及坐标系
3.2 建立平移旋转新坐标系
先进行平移建筑限界坐标,后进行旋转,计算方法如下:󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
3.2.1 建立以曲线下股钢轨中心线为纵坐标的坐标,以轨顶中心为原点建立坐标系󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
在建立新坐标系中,原横坐标平移量为两股钢轨中心线间距S的一半(标准轨距为\(\frac{1500}{2}=750mm\)),即原横坐值标减去750mm,则得到轮廓线各变化点的横坐标值,纵坐标不变。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
3.2.2 建立以曲线下股轨顶中心为轴通过超高进行旋转,进行坐标平移旋转转换。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
已知计算点坐标:假设横坐标X0,纵坐标Y0
坐标平移量:车体中心与线路中心偏离\(W_内=\frac{40500}{R}\),得出横坐标平移量\(X_P=\frac{40500}{R}\),纵坐标平移量\(Y_P=0\)󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
旋转角度:以曲线下股轨顶中心点为轴进行旋转,因曲线超高引起的车体旋转角度\(\theta=\arctan (\frac{h}{2})\),h为曲线超高,S为两股钢轨中心距离,标准轨距为1500mm󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
根据通用坐标平移旋转公式(证明从略)[4],最终铁路建筑限界各变化点坐标的计算公式为:
\(X=\cos (\theta)\times X_0+Y_0\sin (\theta)+X_P\quad(公式4)Y=\cos (\theta)\times Y_0-X_0\sin (\theta)+Y_P\quad(公式5)\)󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
根据公式-4和公式-5对每一个铁路建筑限界轮廓线变化点的坐标进行平移旋转,得到一组全新的铁路建筑限界轮廓线坐标值,表1。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
3.3 绘制建筑物与铁路限界位置关系图
制建筑物与铁路限界位置关系图,需要在统一坐标下,建筑限界轮廓线坐标值和建筑物坐标值。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
3.3.1建筑限界轮廓线坐标值
在以上3.2.2条已完成建筑限界轮廓线坐标值计算,建筑物坐标测量方法如下:󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
3.3.2建筑物坐标值
从轨顶面起分左、右侧,逐一测量设备、建筑物及其他设施每个变化点距线路中心线的水平距离、高度起算高度:直线地段以轨顶面为起算点测量,曲线地段以内轨顶面为起算点测量。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
在以曲线下股钢轨中心线为纵坐标,轨顶中心为原点建立坐标系中,将建筑物和铁路建筑限界廓线坐标按1:1比例绘制成CAD图,根据建筑物廓线和铁路建筑限界轮廓线是否重叠,可判定是否侵限界。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
4 计算实例
以文献为[5]算例进行检算分析,证明绘制CAD铁路限界图判定建筑物是否超限方法的正确性与可靠性:
算例资料:已知某车站低站台面与曲线内侧轨面距离为300mm(距直线建筑限界轮廓垂直距离为50mm),站台帽外沿距线路中心线1820mm(距直线建筑限界轮廓水平距离为95mm)。现场测量及复核表明,站台距线路中心线距离符合设计要求。正线的低站台位于半径为1040m的曲线内侧,曲线超高为130mm。2013年7月,某次旅客列车牵引的SS9G型机车通过此车站时,机车位于曲线内侧的脚蹬与低站台帽发生刮擦,造成列车非正常停车事故。
4.1 车体中部铁路限界坐标绘制CAD铁路建筑限界包络轮廓线
4.1.1建立初始坐标系,计算原坐标值󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
建立以曲线下股钢轨中心线为纵坐标,以下股钢轨顶面水平线为横坐标建立新坐标系,则平移了半个钢轨中心距\(\frac{1500}{2}=750mm\),设各变化点的坐标为Xi和Yi,则原坐标平移后为X’=Xi-750,Y’=Yi。
横坐标平移量:\(X_P=\frac{40500}{R}=\frac{40500}{1040}=39mm\);纵坐标平移量:YP=0
旋 转 角 度:\(\theta=\arctan (\frac{h}{S})=\arctan (\frac{130}{1500})=4^{\circ}57^{‘}11.7^{”}\)󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
根据公式4和公式5,以第5个变化点为例,计算点平移旋转后的坐标值󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$X=\cos (\theta)\times X_0+Y_0 \sin(\theta)+X_P=\cos (4^{\circ}57^{‘}11.7^{”})\times 1125+350\times \sin(4^{\circ}57^{‘}11.7^{”})+39=1190mm\\Y=\cos (\theta)\times Y_0-X_0 \sin(\theta)+Y_P=\cos (4^{\circ}57^{‘}11.7^{”})\times 350-1125\times \sin(4^{\circ}57^{‘}11.7^{”})+0=252mm$$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
其他变化点以此类推计算坐标值,计算结果如表1,同理也可计算车体端部其他变化点坐标值。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
4.2 根据站台控制点A与线路位置关系,在统一坐标系中的坐标值
根据已知资料,站台帽外沿距线路中心线1820mm,站台面与曲线内侧轨面距离为300mm,以曲线下股钢轨中心线为纵坐标,下股钢轨顶面水平线为横坐标建立新坐标系,站台帽外沿控制点A坐标为󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$X_A=1820-\frac{S}{2}=1820-\frac{1500}{2}=1070mm,Y_A=300mm。$$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

图2 车体中部断面CAD建筑限界图
生成的车体中部断面铁路限界坐标表1,按1:1比例绘制CAD铁路建筑限界包络轮廓线图,如图2。
表1 车体中部断面铁路限界坐标表
| 测点编号 | 原坐标(mm) | 平移旋转后坐标(mm) | 坐标差(mm) | |||
| 横坐标X | 纵坐标Y | 坐标X | 坐标Y | 横坐标差 | 纵坐标差 | |
| 1 | 650 | 25 | 689 | -31 | 39 | -56 |
| 2 | 750 | 200 | 803 | 134 | 53 | -66 |
| 3 | 975 | 200 | 1028 | 115 | 53 | -85 |
| 4 | 975 | 350 | 1041 | 265 | 66 | -85 |
| 5 | 1125 | 350 | 1190 | 252 | 65 | -98 |
| 6 | 1125 | 1100 | 1255 | 999 | 130 | -101 |
| 7 | 1620 | 1110 | 1749 | 966 | 129 | -144 |
| 8 | 1690 | 1210 | 1827 | 1060 | 137 | -150 |
| 9 | 1690 | 3000 | 1982 | 2843 | 292 | -157 |
| 10 | 1250 | 4500 | 1673 | 4375 | 423 | -125 |
| 11 | 650 | 5500 | 1161 | 5423 | 511 | -77 |
| 12 | -2150 | 5500 | -1628 | 5665 | 522 | 165 |
| 13 | -2750 | 4500 | -2312 | 4721 | 438 | 221 |
| 14 | -3190 | 3000 | -2880 | 3264 | 310 | 264 |
| 15 | -3190 | 1210 | -3035 | 1481 | 155 | 271 |
| 16 | -3120 | 1110 | -2974 | 1375 | 146 | 265 |
| 17 | -2625 | 1100 | -2481 | 1323 | 144 | 223 |
| 18 | -2625 | 350 | -2546 | 575 | 79 | 225 |
| 19 | -2475 | 350 | -2397 | 562 | 78 | 212 |
| 20 | -2475 | 200 | -2409 | 413 | 66 | 213 |
| 21 | -2250 | 200 | -2185 | 394 | 65 | 194 |
| 22 | -2150 | 25 | -2101 | 211 | 49 | 186 |
| 23 | -1500 | 25 | -1453 | 154 | 47 | 129 |
| 24 | -1500 | 0 | -1455 | 130 | 45 | 130 |
| 25 | 0 | 0 | 39 | 0 | 39 | 0 |
| 26 | 0 | 25 | 41 | 25 | 41 | 0 |
| 27 | 650 | 25 | 689 | -31 | 39 | -56 |
| 站台A点 | 1070 | 300 | 1070 | 300 | 0 | 0 |
4.3 坐标计算及CAD图分析站台侵限情况
根据表1,限界轮廓线第5点经过平移旋转后,X=1190mm,Y=252mm,站台控制点A的坐标为横坐标1820-750=1070mm,纵坐标300mm未变,从坐标数据来看,相对于轮廓线上的5#控制点,站台控制点A水平差1070-1190=-120mm,垂直差252-300=-48mm,横纵坐标均已经超限,如图3。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
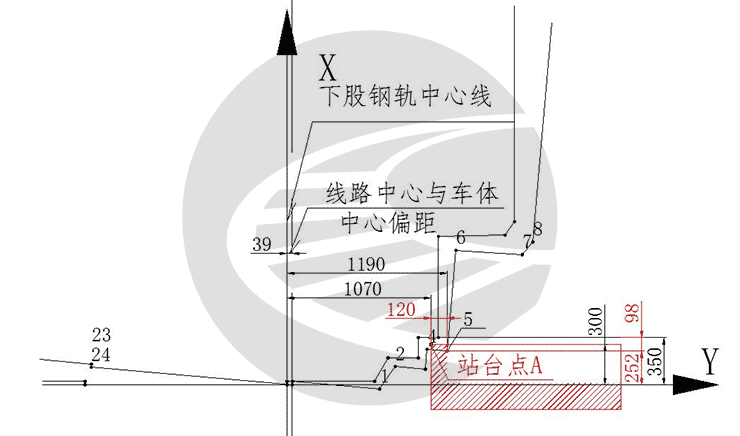
图3 车体中部站台控制点A与建筑限界的位置关系图
通过图3可以看出,站台轮廓线与铁路建筑限界包络轮廓线重叠,侵入建筑限界,造成了机车与站台发生刮擦。
5 结束语
通过以上分析,证明利用本方法绘制限界与建筑物位置关系准确,解决建筑物的任意一点是否与横断面轮廓重叠,虽坐标计算过程较复杂,但通过编写程序迅速完成计算。利用二次开发CAD自动绘制限界及建筑物CAD位置关系图,通过CAD图可直接判定建筑物是否侵入限界。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
本方法还可绘制等高或不等高线间等复杂的建筑限界图,如存在缓和曲线段的偏离距与超高值计算,可参考相关文献 [6] -[7]解决。
文章来源:
原文名称:利用图解法求曲线地段建筑限界加宽的方法󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
文章作者: 廖显军
作者信息:中国铁路南宁局集团有限公司󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄣󠄤󠄞󠄢󠄥󠄣󠄞󠄡󠄩󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
参考文献:[s][p]
- [1] 陈知辉.铁路曲线轨道 (第二版) [M]. 北京 中国铁道出版社 2016
- [2] 中国铁路总公司.(TG/01—2014) 铁路技术管理规程(普速铁路部分)[ s].北京:中国铁道出版社 2014
- [3] 国家标准局. TB 10099-2017 铁路车站及枢纽设计规范[ s].2017.
- [4] 陈家驹.铁路曲线弦绳法定位 [M]. 成都 :西南交通大学出版社 2012
- [5] 龙科.关于细化铁路曲线上建筑限界加宽的建议[J].铁道技术监督,2014(1):2-4
- [6] 赵振刚.铁路建筑限界缓和曲线地段加宽研究 [J]铁道标准设计2017.5:16-22
- [7] 李明炜.对铁路站场到发线曲线地段建筑限界加宽方法的探讨[J].铁道标准设计2017.2:10-13
[/p]




