[图文]铁路曲线地段限界加宽推导及计算方法

1 建筑接近限界

在铁路线路上，为确保行车安全和人身安全，机车车辆及其装载的货物不得超越一定的轮廓线，此轮廓线称为机车车辆限界。另外，靠近轨道的建筑物及设备不得侵人其线路的轮廓线，此轮廓线称为建筑接近限界。上述两种限界之间存在一定的空间间隔。

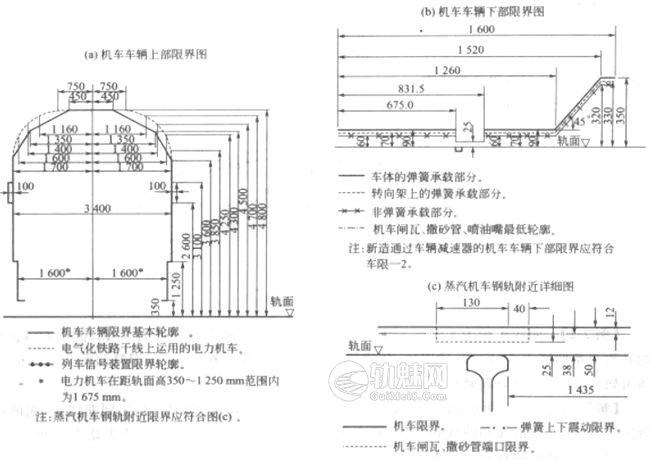
图1 机车车辆限界

图2 直线建筑接近限界

建筑接近限界包括直线建筑接近限界(简称建筑接近限界)、隧道建筑限界及桥梁建筑限界。图1为机车车辆限界，图2为直线建筑接近限界。

建筑接近限界半宽为2440mm,这是考虑到最大货物超限装载限界的半宽为2225mm,货物振动横移量为170.5mm,安全量为44.5mm,则

建筑接近限界半宽=2225+170.5+44.5=2440 ( mm )

建筑接近限界的高度为5500mm，这是考虑到超限货物装载限界高度为5300mm,货物向上振动偏移量为46.5 mm，安全量为153.5 mm,则

建筑接近限界高度=5300+46.5+153.5=5500 ( mm )

在电力机车牵引的线路上，建筑接近限界的最大高度为6550mm，困难时可为6200 mm。这是考虑到线路上空有输电接触网。

2 曲线上建筑接近限界的加宽

列车在曲线上运行时，转向架可以转动，而转向架上的车体为刚性结构，不能随轨道而弯曲，车体纵向轴线与轨道中心线不相吻合，致使车体两端向轨道外侧突出，车体中部向轨道内侧偏入，使车体与建筑接近限界间的净空减少。另外，由于曲线外轨设置超高，车体向曲线内侧倾斜，也会影响内侧限界。所以，曲线地段的建筑接近限界较直线地段的大，应在直线建筑接近限界的基础上适当加宽。

1.曲线限界内侧加宽

图3 车体向轨道内侧偏移图                                 图4 外轨超高引起车体向内侧偏移

由图3、图4可知，曲线上建筑接近限界的加宽，与车体长度，两转向架间的距离、曲线半径及外轨超高有关。

1)平面内侧加宽W_平内

从平面上看，如图3所示，车体平面纵向轴线的中部向轨道中心线内侧偏入，车体中部内侧偏移量为ƒ=l²/8R。式中，l为转向架中心销距。我国最长的车辆，其车体长为26m，转向架中心销距l=18m，代入上式即可求出平面内侧加宽值:

$$W_{平内}=\frac{18^2}{8R}\times 1000=\frac{40500}{R}\quad（mm）$$

2)立面内侧加宽W_立内

从立面上看，如图4所示。因外轨设置超高，致使车体向内倾斜，车体内侧面的，上部明显偏人曲线内侧,由此而引起的立面内加宽W_立内存在如下关系:\(\frac{W_{立内}}{H}=\frac{h}{S_1}\)，式中，H为自轨面至建筑物计算点的高度。将S=1500 mm代入，即得

$$W_{立内}=\frac{H}{1500}\cdot h $$

3)曲线限界内侧总加宽量W_内

$$W_{内}=W_{平内}+W_{立内}=\frac{40500}{R}+\frac{H}{1500}h$$

2.曲线限界外侧加宽

由图3可知，车体纵向轴线的两端向轨道中心线外侧突出,其突出的距离即为曲线限界外加宽之值

$$W_外=\frac{L^2}{8R}-\frac{l^2}{8R}=\frac{26^2}{8R}\times 1000-\frac{18^2}{8R}=\frac{44000}{R}\quad（mm）$$

3.曲线线间距加宽

曲线线间距加宽是指曲线两端的线间距均为最小线间距时，曲线上的线间距在最小线间距基础上所需要的加宽量。

1)外侧线的超高大于内侧线的超高时

由于外侧线路上的车辆内倾，在立面上车辆上部间的净空减小了，而内侧线路上的车辆内倾，却使车辆上部间的净空增大。因此，线间距加宽应为外侧线限界内加宽加上内侧线限界外加宽，即

$$W_{线间}=W_{内}+W_{外}-W_{立内}\\=\frac{40500}{R_{外}}+\frac{H}{1500}h_{外}+\frac{44000}{R_{内}}-\frac{H}{1500}h_{内}$$

将H=3600 mm代人，得h_外>h_内时的线间距加宽公式为

$$W_{线间}=\frac{40500}{R_外}+\frac{44000}{R_内}+2.4（h_外-h_内）\quad（mm）$$

2)内侧线的超高大于或等于外侧线的超高时

由于两线路上的车辆上部间的净空加大，线间距加宽由外侧线的平面内侧加宽和内侧线的外侧加宽决定，即

$$W_{线间}=\frac{40500}{R_外}+\frac{44000}{R_内}\quad（mm）$$

上述各式计算出的加宽量，均应进整成5mm的倍数。

文章来源：

刘兴文主编.西南交通大学出版社《铁路轨道》2011

何奎元主编《铁路轨道与修理》2008