曲线曲率的含义及计算公式

在工程技术中，有时需要考虑曲线的弯曲程度.例如,设计铁路线路时,如果弯曲程度不合适，很容易造成火车出轨等事故；又如，车床的主轴由于所受荷载与它本身的重量的作用，总会产生弯曲变形，如果弯曲程度过大，就会影响车床的正常运转和精度，为了刻画曲线的弯曲程度,本节讨论曲线的曲率。

一、曲率

先从几何图形直观地分析曲线的弯曲程度是由哪些量来确定的。

当动点沿曲线弧由点M移动到点N时,动点处的切线也相应地跟着转动,切线转过的角称为转角，用α表示.可以看出

(1)如果两弧的长度相等,那么转角大的,曲线弧的弯曲程度也大,转角小的,曲线弧的弯曲程度也小[图1-(1)]。

(2)如果两弧的切线转角相等,那么弧较长的,它的弯曲程度反而小,弧较短的，弯曲程度反而大[图1-(2)]。

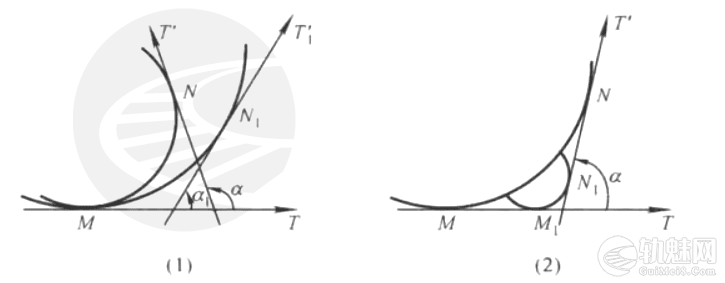
图1

综上分析可知:弧的弯曲程度可用弧两端切线的转角与弧长之比的绝对值|α÷MN|来描述，这个值越大,弧的弯曲程度就越大,这个值越小,弧的弯曲程度就越小。

我们把弧两端切线的转角与弧长之比的绝对值,称为这段弧的平均曲率,记为\(\overline{K}\)，既

$$\overline{K}=\left | \frac{a}{\widehat{MN}} \right |$$

一般地曲线的弯曲程度随点而异，所以弧的平均曲率，只能表示整段弧的平均弯曲程度。显然，当弧越短时，平均曲率就越能近似地表示弧上某一点附近的弯曲程度。下面给出曲线在一点曲率的定义。

定义：当点N沿曲线趋近于点M时,\(\widehat{MN}\)的平均曲率的极限,称为曲线在点M的曲率（curvature)，记为K，即

$$K=\lim_{MN\rightarrow 0}\left | \frac{\mathrm{a} }{\mathrm{\widehat{MN}}} \right |$$

注意(1）因为只考虑曲线弯曲程度的大小,所以曲率K只取非负值;

(2）曲率的单位为:弧度/单位长.

例1 已知圆的半径为R,求圆上:(1)任一段弧的平均曲率;(2)任一点处的曲率。

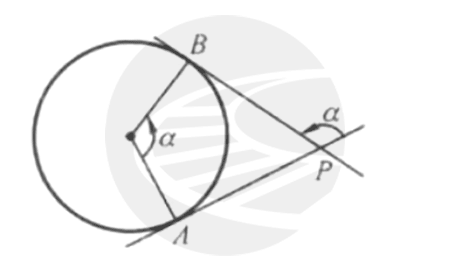
图2

解(1）如图2所示,在圆上任取一段弧\(\widehat{AB}\),由平面几何知道,弧两端切线AP与BP的转角α等于圆心角,即∠AOB= α,于是\(\widehat{AB}\)=Rα ,因此,\(\widehat{AB}\)的平均曲率为

$$\bar{K}=\left | \frac{a}{\widehat{AB}} \right |=\frac{a}{Ra}=\frac{1}{R}$$

(2）圆上任一点的曲率\

$$K=\lim_{\widehat{AB}\rightarrow 0}\left | \frac{a}{\widehat{AB}} \right |=\lim_{\widehat{AB}\rightarrow 0}\frac{1}{R}=\frac{1}{R}$$

这就是说,圆上任一段弧的平均曲率及圆上任一点的曲率都相等,而且等于半径R的倒数\(\frac{1}{R}\)。即圆的弯曲程度处处一样，半径越小，曲率越大，弯曲得越厉害。

以下我们给出曲线y=ƒ(z)上任意点处的曲率计算公式。

设函数y=ƒ(z)具有二阶导数,则曲线y=ƒ(z)在任意点M(z，y)的曲率计算公式为

$$K=\frac{\left |{y}” \right |}{\left ( 1+{y}’^{2} \right )^{\frac{2}{3}}}$$

(推导略)

[思考]由上面的公式能否得出：直线上每点处的曲率为零；二阶可导函数曲线上拐点处的曲率也为零。为什么?

如果ly’l比1小得多，记为\(\left |{y}’ \right |\ll 1\),于是\(1<1+{y}’^2\ll 2\),因此(1＋y’²)^3/2≈1,由曲率计算公式得K≈|y”|，这个近似公式在工程技术中常用到。

例2 求曲线y= ax³(a > 0,x≥0)的曲率K及\(K|_{x=0}\)

解 由y= ax³，得y’= 3ax²，y”=6ax，代入曲率计算公式,得

$$K=\frac{6ax}{\left (1+9a^2x^4\right )^{\frac{3}{2}}},K=|_{x=0}=0$$

例3 求曲线\(y=2ln(1-\frac{x^2}{4})\)上曲率最大的点及最大曲率。

图3

解 函数的定义域为(-2，2)。讲\({y}’=-\frac{4x}{4-x^2},{y}”=-\frac{4+(4+x^2)}{(4-x^2)^2}\)，代入曲率计算公式，得

$$K=\frac{\left | -\frac{4(4+x^2)}{4(4+x^2)}\right |}{\left [ 1+(-\frac{4x}{4-x})^2\right ]^\frac{3}{2}}=\frac{\frac{4(4+x^2)}{(4-x^2)^2}}{\left [ \frac{(4+x^2)^2}{(4-x^2)^2}\right ]^\frac{3}{2}}\qquad(-2<x<2)$$

求导数，得

$${K}’=4\cdot \frac{-2x(4+x^2)^2-(4-x^2)\cdot 2(4+x^2)\cdot 2x}{(4+x^2)^3}=\frac{8x(12-x^2)}{(4+x^2)^3}$$

令 K’=0，得x=0，\(x=\pm 2\sqrt{3}\)（舍去）。

由于曲率K的最大值存在,而现在函数在(-2，2)内只有一个驻点,因此当x =0时,函数K取得最大值。因为x=0时y=0 ，所以在点(0，0)处,曲线\(y=2ln(1-\frac{x^2}{4})\)的曲率最大,最大曲率为1。

这里求曲率最大点也可以不用求导法。在\(K=\frac{4(4-x^2)}{(4+x^2)^2}\)中，显然，当x=0时，分子最大而分母最小，因而这时K最大。

由曲率计算公式和初等函数的连续性知，如果一阶、二阶导数y’、y”都连续，则曲率K也连续.如图3所示的曲线轨道BAM(其中,\(\widehat{AM}\)是一段圆弧，直线BA与弧\(\widehat{AM}\)相切于点A)，在点A处的曲率是不连续的(因直线上各点处的曲率为零；而圆弧上各点处的曲率为1/R)，当火车行驶在曲率不连续的点A时，就要产生一个冲动。所以在铁路线路设计时，要用一条缓和曲线(曲率连续变化的曲线)来连接直线段与曲线段，使其在与直线轨道连接处的曲率为零，而在与曲线轨道连接处，曲率应等于曲线轨道在该点处的曲率，通常选用三次抛物线作为这过渡曲线。

例4 如图4所示，BO为直线铁路轨道,\(\widehat{AM}\)为半径为R的圆弧铁路线路，试选定适当的参数a(a>0)，使曲线y = ax³的弧段\(\widehat{OA}\)(其长为L)可作为连接这两段线路的过渡曲线线路。

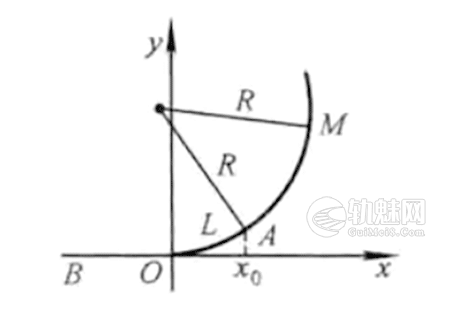
图4

解 由例2知，\(K=\frac{6ax}{\left (1+9a^2x^4\right )^{\frac{3}{2}}}\),且在O(0，0)处,K₀=0。

$${K}’=\frac{6a(1-45a^2x^4)}{(1+9a^2x^4)^\frac{5}{2}},令{K}’=0，得x_1=\sqrt[4]{\frac{1}{45a^2}}$$

要使曲线OA成为连接直线线路BO与圆弧线路\(\widehat{AM}\)的过渡曲线，应K_A=1/R。通过选定适当的参数,使x₀∈[0，x₁]，这样在区间[0，x₀]上，曲率K从0连续单调增加到1/R。当ly’|≪1时，由曲率计算近似公式及例2,得K_A~≈6ax₀=1/R，于是\(a= \frac {1}{6Rx_0}\)。注意到|y’|≪1，此时有

$$\left | {y}’ \right |_{x=x_0}|=3ax_{0}^{2}=\frac{3ax_{0}^{2}}{6Rx_0}=\frac{1}{2}\cdot \frac{x_0}{R}\ll 1$$

因此\(\frac{L}{R}\ll 1,a=\frac{1}{6RL}\)。

所以，当L/R≪1时,曲线 \(y= \frac {x^3}{6RL}\)可作为连接BO、弧\(\widehat{AM}\)两线路的过渡曲线。

 二、曲率圆和曲率半径

用曲率的计算公式,可以求出曲线y =f(x)在任一点的曲率。为了使曲率直观形象,也可以用图像来表示曲率。

如果曲线L: y =ƒ(x)在某点M(x，y)的曲率K不等于零,由例1可知,曲线在点M的曲率,与半径为1/K的圆的曲率相等,因此,我们把曲率K的倒数

$$R=\frac{1}{K}=\frac{\left (1+{y}’^2 \right )^{\frac{3}{2}}}{\left | {y}”\right |}$$

称为曲线L在点M的曲率半径(radius of curvature)。

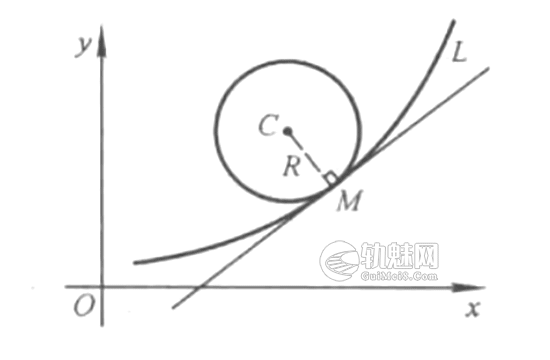
图5

作曲线L在点M的切线与法线，在法线上曲线的凹侧取点C，使MC的长等于曲线在点M的曲率半径R，即|MC|=R。点C称为曲线L在点M的曲率中心( center of curvature)。以C为圆心，以R为半径的圆称为曲线L在点M的曲率圆( circle of curvature)(图5)。设曲线y=ƒ(x)在点M(x，y)处的曲率中心为C(α，β),则

$$a=x-\frac{{y}’\left ( 1+{y}’^2\right )}{{y}”},\qquad\beta =y+\frac{\left ( 1+{y}’^2\right )}{{y}”}$$

例5 设工件内表面的截线为抛物线y=0.4x²(图6)，现在要用砂轮磨削其内表面，问用直径多大的砂轮比较合适？并求出抛物线在点(1，0.4)处的曲率中心。

图6

解 显然,我们选用的砂轮的半径,应小于或等于工件的内表面截线上各点处的曲率半径的最小值，否则就会磨掉工件的不应磨去的部分。因此我们先求曲率半径的最小值。由于\({y}’=0.8x,{y}”=0.8\)，所以，工件内表面截线y= 0.4x²上任意一点的曲率半径为

$$R=\frac{\left ( 1+0.64x^2\right )^\frac{3}{2}}{\left | 0.8\right |}=\frac{\left ( 1+0.64x^2\right )^\frac{3}{2}}{ 0.8}$$

容易看出，当x=0时，即在抛物线y=0.4x²的顶点处，R的值最小，这个最小值R_min=1.25，因此我们应选用直径等于或略小于2.5单位的砂轮磨削工件内表面才比较合适。

由于在点(1，0.4)处,\({y}’|_{x=1}=0.8,{y}”|_{x=1}=0.8\)，所以

$$a=1-\frac{0.8\left ( 1+0.64\right )}{0.8}=-0.64,\qquad\beta =0.4+\frac{\left ( 1+0.64\right )}{0.8}=2.45$$

因此,抛物线在点(1，0.4)处的曲率中心为(-0.64，2.45)。

文章来源:

杜吉佩主编；工程类应用数学基础教程编写组编《应用数学基础教程 工程类》 2004年版

[/reply]