预制梁场龙门吊计算书

1 工程概况

1.1 工程简介

本项目预制梁板形式多样，分别为预制箱梁、空心板及T梁，其中最重的是30m组合箱梁中的边梁，一片重达105t。预制梁场拟采用两台起吊能力为100t的龙门吊用于预制梁的出槽，其龙门吊轨道之间跨距为36.7m。

1.2 地质情况

预制梁场基底为粉质粘土。查《路桥施工计算手册》中碎石土的变形模量E₀=29～65MPa，粉质粘土16～39MPa，考虑最不利工况，统一取粉质粘土的变形莫量E₀=16 MPa。临建用地经现场动力触探测得实际地基承载力大于160kpa。

2 基础设计及受力分析

2.1 龙门吊轨道基础设计

龙门吊轨道基础采用倒T型C30混凝土条形基础，基础底部宽80cm，上部宽40cm。每隔10m设置一道2cm宽的沉降缝。基础底部采用8根Φ16钢筋作为纵向受拉主筋，顶部放置4根Φ12钢筋作为抗负弯矩主筋，每隔40cm设置一道环形箍筋。，箍筋采用HPB235Φ10mm光圆钢筋，箍筋间距为40cm，具体尺寸如图1.2.1-1、1.2.1-2所示。

图1.2.1-1-龙门吊轨道基础设计图

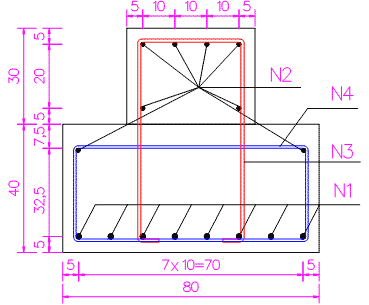
图1.2.2-2 龙门吊轨道基础配筋图

2.1 受力分析

梁场龙门吊属于室外作业，当风力较大或降雨时候应停止施工。当起吊最重梁板（105t）且梁板位于最靠近轨道位置台座的时候为最不利工况。

图1.2-1 最不利工况所处位置

单个龙门吊自重按G₁=70T估算，梁板最重G₂=105t。起吊最重梁板时单个天车所受集中荷载为P，龙门吊自重均布荷载为q。

P=G₁/2=105×9.8/2=514.5KN                 （1-1）

q=G₂/L=70×9.8/42=16.3KN/m                （1-2）

当处于最不利工况时单个龙门吊受力简图如下：

图1.2-3 龙门吊受力示意图

龙门吊竖向受力平衡可得到：

N1+N2=q×L+P                 （1-3）

取龙门吊左侧支腿为支点，力矩平衡得到：

N2×L=q×L×0.5L+P×3.5            （1-4）

由公式（1-3）（1-4）可求得N1=869.4KN，N2=331.1KN

龙门吊单边支腿按两个车轮考虑，两个车轮之间距离为6m，对受力较大支腿进行分析，受力简图如下所示：

图1.2-4 支腿单车轮受力示意图

受力较大的单边支腿竖向受力平衡可得

N1=N+N                   （1-5）

由公式（1-5）得出在最不利工况下，龙门吊单个车轮所受最大竖向应力为N=434.7KN

3 建模计算

3.1 力学模型简化

对龙门吊轨道基础进行力学简化，基础内力计算按弹性地基梁计算，用有限元软件Midas Civil2015进行模拟计算。即把钢筋砼梁看成梁单元，将地基看成弹性支承。

图1.3-1 力学简化模型

3.2弹性支撑刚度推导

根据《路桥施工计算手册》p358可知，荷载板下应力P与沉降量S存在如下关系：

       (1-6)

其中：

E0——地基土的变形模量，MPa；

ω——沉降量系数，刚性正方形板荷载板ω=0.88；刚性圆形荷载板ω=0.79；

ν——地基土的泊松比，为有侧涨竖向压缩土的侧向应变与竖向压缩应变的比值；

Pcr——p-s曲线直线终点所对应的应力，MPa；

s——与直线段终点所对应的沉降量，mm；

b——承压板宽度或直径，mm；

不妨假定地基的变形一直处在直线段，这样考虑是比较保守也是可行的。故令地基承载的刚度系数

则：

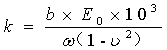
另考虑到建模的方便和简单，令b=200mm（纵梁向20cm一个土弹簧），查表得粉质粘土ν_n=0.25～0.35，取ν=0.35粉质粘土的变形莫量E₀=16 MPa。带入公式(1-6)求解得：

K=4.144×10⁶

3.3 Madis2015建模计算

（1）模型建立

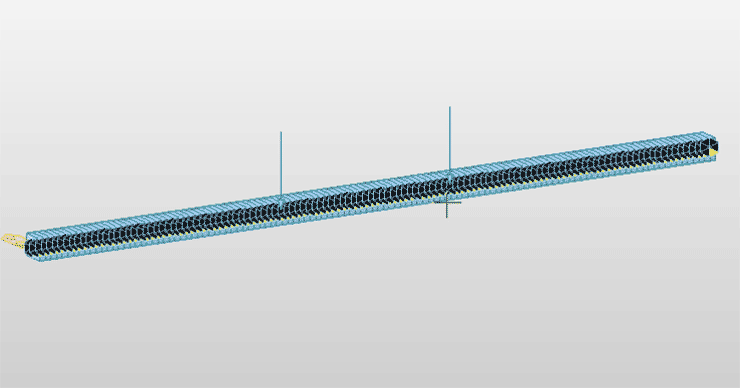
图1.3-2 模型建立

（2）龙门吊轨道梁弯矩计算

图1.3-3 轨道梁应力图

（3）轨道梁剪力计算

图1.3-4 轨道梁剪力图

（4）基地反力计算

图1.3-5 基地反力图

（5）轨道梁位移

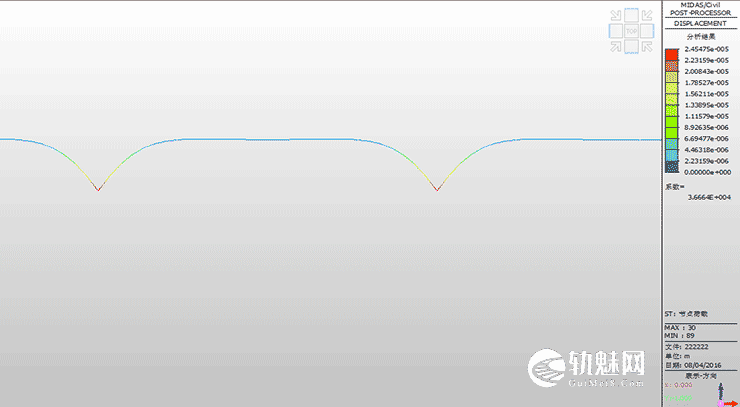
图1.3-6 轨道梁位移图

经过Madis2015建模计算，求得龙门吊轨道梁最大应力弯矩为279.6KN·m，最大负弯矩为64.9KN·m，最大剪力207.6KN，土弹簧最大支点反力14.4KN，考虑到轨道梁位移很小，土弹簧处于弹性变形过程，通过图1.3-5可知基地承载范围在纵梁方向集中在12m。

4 龙门吊轨道梁配筋计算

4.1 轨道梁正截面强度验算

（1）判断是截面形式

单筋截面适筋梁最大承受能力为:

  M_u=ƒ_cdh₀²ζ_b(1-0.5ζ_b)       (1-7)

       h₀=h-a_s    （1-8）

ƒ_cd——混凝土抗压强度设计值，C30混凝土取14.3Mpa；

h₀——截面有效高度；

a_s ——纵向受拉钢筋全部截面重心至受拉边缘的距离（轨道梁设计=7.5cm）；

b——受压区混凝土截面宽度，取400mm；

ζ_b——相对受压区高度，取0.56；

由公式（1-7）（1-8）可以求的；

M_u=14.3×10³×0.4×0.625×0.625×0.56×(1-0.5×0.56)=830KM·m

因为M_u≥γ₀M_u=1.1×279.6=307.56，故龙门吊轨道梁单筋截面就满足受力情况。

（2）最小配筋面积计算

通过截面力矩平衡、受力平衡可得：

式（1-9） 

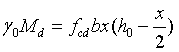
式（1-10）

式（1-11）

ƒ_cd——钢筋抗拉强度设计值，取280Mpa；

A_s——受拉区钢筋截面面积；

x——计算受压区高度；

γ₀——结构重要性系数，取1.1。

通过公式（1-10）可求得x=42.78mm

通过公式（1-11）可求得：

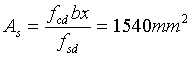
结论：纵向受拉钢筋最小配筋率为1540mm²，龙门吊轨道梁实际配置8根Φ16纵向受拉钢筋A_{s（实际）}=1600mm²大于最小配筋率，故正截面强度验算符合要求。[reply]

4.2 斜截面强度计算

根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62-2004）可知，混凝土和箍筋共同抗剪能力的公式为

α₁——异号弯矩影响系数，计算简支梁和连续梁近边支点梁段的抗剪承载力时，α₁=1.0；计算连续梁和悬臂梁近中间支点梁段的抗剪承载力时，α₁=0.9；故取α₁=1.0；

α₂——预应力提高系数，对钢筋混凝土受弯构件，α₂=1.0；对预应力混凝土受弯构件，α₂=1.25，但当由钢筋合力引起的截面弯矩与外弯矩的方向相同，或允许出现裂缝的预应力混凝土受弯构件，取α₂=1.0；故取α₂=1.0；

α₃——受压翼缘的影响系数，取α₃=1.1；

b——斜截面受压端正截面处矩形截面宽度，取b=400 mm；

h₀——斜截面受压段正截面的有效高度，自纵向受拉钢筋合力点至受压边缘的距离；故取h₀=625mm；

p——斜截面内纵向受拉钢筋的配筋百分率，p=100ρ，当p>2.5时，取p=2.5，其中ρ=A_s/bh₀；故p=100×1005/(400×625) =0.402；

f_cu,k——边长为150mm的混凝土立方体抗压强度标准，取f_cu,k =30MPa,；

ρ_sv——斜截面内箍筋配筋率，ρ_sv= A_sv/（S_vb）=157.1/（500×400）=0.079%；

f_sv——箍筋抗拉强度设计值，箍筋采用光圆钢筋，故取值f_sv=195MPa；

A_sv——斜截面内配置在同一截面的箍筋各肢的总截面面积，取157.1mm²；

S_v-——斜截面内箍筋的间距，取500mm。

由上述条件可以求得：

=170KN＞166.5KN（最大剪力）

故轨道梁400mm设置一道环形φ10箍筋满足斜截面受力要求。

4.3 轨道地基承载力计算

经过Madis2015建模可以看出，在纵梁方向基地土弹簧反力范围为2.2～2.4m，考虑端头位置反力较小，出于保守考虑纵梁方向2m为基底承力范围。轨道梁下方设置50cm碎石垫层，地基压力按45度角扩散至基地，纵梁地基承力范围为3m。

图1.4-1 轨道梁地基承载范围侧面图

图1.4-2 轨道梁地基承载范围立面图

考虑最不利工况，轨道梁所受最大压力为：F_max=411.23KN

地基承力面积：S=3×1.2=3.6m²

对地基压力:

ƒ_max=F_max÷S=114.2kpa＜160kpa（实测地基承载力）

故龙门吊轨道基础地基承载力满足要求。

[/reply]