地铁车站顶部龙门吊轨道基础设计计算

1 工程概况

广州地铁二号线赤岗~鹭江区间隧道采用盾构法施工,盾构机始发场地设在赤岗站。赤岗地铁车站为一地下两层的钢筋混凝土结构,顶板横向净跨距16.3m,厚度0.8m,顶板下无梁无柱,其上覆盖一层1.2m厚的人工填土,填土层表面与天然地面平齐。设计给定的顶板上方地面允许施工荷载为20kN/m²,考虑到顶板上有1.2m厚的人工填土层,填土密度按P=2g/cm³计,可推算出顶板的直接允许荷载为44kN/m²。根据施工场地布置,顶板上方地表沿左右线隧道轴线方向平行布置了两台重型龙门吊,以供盾构施工过程渣土、管片、砂浆等物料上下井之用。龙门吊的一根轨道基础铺设在靠近车站侧墙的一排管桩上,另一根轨道基础铺设在车站顶板跨中上方的填土层上,而龙门吊的两根轨道之间的场地计划作为隧道管片堆放场,见图1。

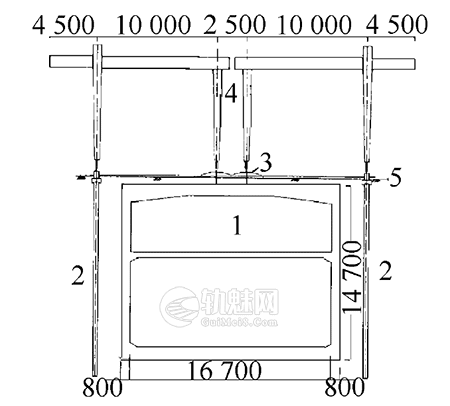
图1 地铁车站顶龙门吊的布设
1-车站主体结构;2-管桩;3-轨道基础;4-龙门吊;5-地面

根据施工场地布置,车站顶板上方将承受相当大的施工荷载,计划正常施工荷载将达30kN/m²,比设计给定的地面允许荷载大10kN/m²。为满足施工要求,保证车站顶板结构的安全,对车站顶板进行了加固,加固后的车站顶板允许荷载为54kN/m²。顶板上方管片堆放区的荷载可作为分布荷载,其大小易于控制,而龙门吊的轮压产生的是集中荷载,如何保证轮压经过轨道基础和人工填土层后扩散到顶板的荷载小于30kN/m²,是轨道基础设计首先要解决的问题。

2 车站顶板上部龙门吊轨道基础设计计算

2.1 计算荷载

图2 轨道反力计算简图

根据施工场地布置,龙门吊悬臂位于车站侧墙外,龙门吊每次起吊管片3块,最大荷重约120kN。当重物沿龙门吊横梁移动到内侧时(吊勾极限位置距立柱1.6m),龙门吊右侧轨道(靠近顶板中央)荷载反力最大,其受力简图见图2。

对图中A点取力矩平衡得:

9.124R₂-(9.124-1.6)P=0

式中,R₂为吊重P产生的轨道反力,由两个轨道轮分担。将最大荷重值P=120kN代入式(1)求得:

R₂=99kN

起吊或制动过程重物会产生动载,按起重机设计规范(GB3811-83),动载系数ψ₂取值如下:

ψ₂=1+0.7v

式中,v为最大起升速度,v=0.12m/s。

考虑动载效应后的单个轮压为:ψ₂R₂/2=53.6kN;龙门吊自重700kN,由4个轨道轮分担,单个轮压为175kN;因此,最大轮压为228.6kN;考虑一定安全余量,取车站顶板上方轨道基础最大设计轮压为230kN。

2.2 计算模型及参数

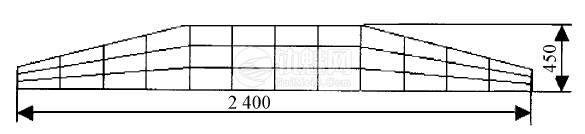
图3 车站顶板上部龙门吊基础横截面

为了使龙门吊轮压在顶板上产生的分布荷载小于设计控制荷载,拟在轨道下设置一条钢筋混凝土基础,基础下保留75cm厚的人工填土层,以作为缓冲和扩散荷载之用。经对多种方案的对比,确定出的基础横截面形状见图3。

将轨道基础看作弹性地基梁,由于基础下方填土层厚仅75cm,地基反力系数不能反映土层厚度对基底应力分布的影响,因此地基弹簧刚度不宜简单套用地基反力系数进行计算,为此将土层离散为土柱,采用土层的压缩模量计算地基弹簧刚度:

k =EA/L        (3)

式中

E——人工填土层的弹性模量,根据地质资料取E=1.5kPa;

A——单个土柱截面积(其大小与基础有限单元面积相等),A=150cm²;

L——土柱高度,L=75cm。

将上述数据代入式(3)得:k=3kN/cm。

采用大型结构分析有限元软件Algor12进行三维分析,土层对基础的作用以土弹簧模拟,车站顶板所受压力等于土弹簧压力。根据圣维南原理,某个力系仅对力作用点附近的一定范围内的应力分布有影响,为减少单元,仅取一个轨道轮作用点前后各3m长的基础进行分析。采用6面体实体单元,共划分4865个单元,6150个节点,最大单元尺寸10cm×10cm×15cm,基础有限元分析模型见图3。材料(C30混凝土)本构模型采用线弹性模型,其参数取值如下:

弹性模量E=30000MPa,μ=0.15,密度ρ=2.4g/cm³。

2.3 计算结果及配筋

1)基底压力分布

轨道轮下方基底压力最大,其值达32.8kPa,考虑0.75m厚土层的自重后,顶板上的最大压应力为47.8kPa<54kPa,符合要求,见图4。

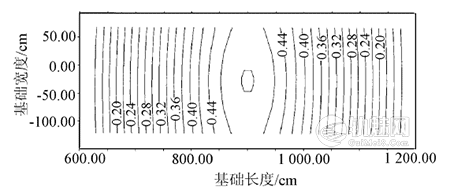
图4 龙门吊基础基底应力分布( 图中应力单位为10²kPa)

从扩散范围看,基底压力是以轨道轮作用点为中心,沿四周逐渐降低。沿轨道轴向距轨道轮作用点2m和3.0m处,基底压力分别降至17.7kPa和6.6kPa,6.6kPa相当于基础自重产生的压力,因此单个轨道轮的轴向应力扩散半径约为2.8m,而龙门吊前后两个轨道轮的轴距为10m,左右轮距为9.124m,因此相邻轨道轮之间的应力叠加作用可忽略不计。

2)基础变形分布

轨道轮作用点下方的竖向位移最大(1.7mm),沿轨道纵向距轨道轮作用点3m处,竖向位移降低至0.3mm,由此可推算出基础的竖向挠度为1.4mm。因此,轮压引起的基础变形不会对龙门吊的运行造成不利影响。

3)基础轴向应力分布

基础上部为受压区,受压区高度约22cm,最大压应力10.2MPa,小于C30混凝土的弯曲抗压强度16.5MPa,因此受压区只需按构造配筋。

基础下部为受拉区,最大拉应力4MPa,由受拉区应力分布积分求得受拉区总拉力约为816kN。按照钢筋混凝土构件受拉区应力全部由钢筋承担的原则,选用∃级钢筋,其强度设计值ƒ_y=310MPa,所以钢筋总面积A_s=2632mm²,折合Φ20Ⅱ级钢筋8.38根,实际取9根。

4)基础横向应力分布

基础上部约2/3为受压区,最大压应力9.2MPa,小于C30混凝土的弯曲抗压强度16.5MPa,因此横向受压区也只需按构造配筋。

基础下部为受拉区,横向受拉区面积远小于轴向受拉区面积,最大拉应力约2.1MPa,由受拉区应力分布积分求得的单位长度受拉区总拉力约为13kN/m,因此横向受拉区也只需按构造配筋。基础宽度2.4m,高0.45m,横向受拉区可按板配置分布筋,单位长度分布钢筋截面积取受力主筋截面积的12%^[1],即:A_f=131.6mm²/m。选用Φ6Ⅰ级配筋,单根钢筋截面积A₁=28.3mm²,则单位长度需配置A_f/A₁=4.65根分布筋,取5根,分布筋间距s=0.2m。

3 车站结构外侧龙门吊桩基轨道梁设计计算

3.1 计算荷载

当重物沿龙门吊横梁移动到最外侧(悬臂端)时,龙门吊左侧轨道荷载反力最大,其受力简图见图5。

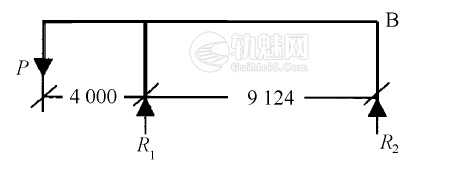
图5 轨道反力计算简图

对图中B点取力矩平衡得:

9.124R₁-(4+9.124)P=0       (4)

式中,R1为吊重P产生的轨道反力,由两个轨道轮分担。

将最大荷重值P=120kN代入式(4)求得:

R₁=172.6kN

考虑动载效应和龙门吊自重后的单个轮压为:

175+ψ₂R₁/2=268.6kN

考虑一定安全余量,取轨道梁最大设计轮压为:300kN。

3.2 计算模型及参数

[reply]

龙门吊左侧轨道梁架设在间距6m的Φ400预应力管桩上,两根管桩之间的轨道梁下方为人工填土,因其不密实,固结时间太短,忽略其对轨道梁的支撑作用。由此将轨道梁简化为支撑于管桩上的多跨连续梁,管桩简化为弹性支座,见图6。

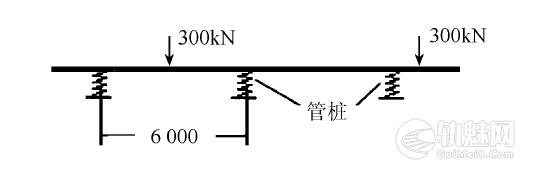
图6 多跨连续梁模型

管桩的压缩刚度k为:

k=EA/L

式中

E——管桩的弹性模量,取C25混凝土弹性模量值E=28000MPa;

A——管桩截面积,A=0.1256m²;

L——桩长,15~18m,取L=18m。

将上述数据代入式(5)得:k=300000kN/m。

3.3 设计结果

当轨道轮作用于梁跨中央时,梁的弯矩最大,根据图6计算模式,轨道梁内力及截面设计计算结果如下:

轨道梁设计截面尺寸300mm×600mm,采用C25混凝土,最大弯矩320kN·m,最大挠度4.9mm,最大剪力250kN,内力分布见图7。

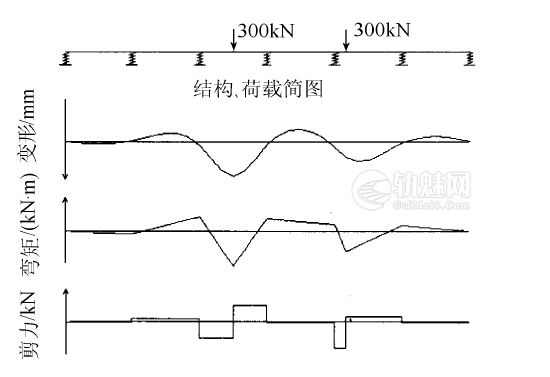
图7 轨道梁内力分布

1)正截面按抗弯配筋

受拉侧配置5根Φ25Ⅱ级钢筋,钢筋保护层厚度30mm;受压侧按构造配筋,上角部各配Φ10Ⅰ级架立筋1根。

2)轨道梁变形校核

参照提升钢井架规范,梁的允许挠度为:

δ_max=L/600=10mm>4.9mm,所以梁的最大变形符合要求。

3)斜截面抗剪设计

根据规范,集中荷载作用下矩形梁混凝土和箍筋的最小承载力为^[3]:

$$V_{min}=\left ( \frac{0.2}{\lambda +1.5}+0.025\right )f_cbh_0$$

式中

V_min——混凝土和箍筋的最小承载力,N;

f_c——混凝土轴心抗压强度设计值,12.5MPa;

b——梁宽度,300mm;

h₀——梁有效高度,570mm;

λ——剪跨比,λ=（a÷h₀）=5.26>3,取λ=3。

所以 V_min=148437N<250000N

最小承载力小于设计剪力,故应按计算配筋,箍筋用量为:

$$\frac{A_{sv}}{S}=\frac{V-\frac{0.2}{\lambda +1.5}f_cbh_0}{1.25f_yh_0}=1.036$$

式中

A_sv——单肢箍筋截面积,mm²;

s——箍筋间距,mm。

选用2Φ8,则单肢箍筋面积A_sv=100.5mm²

由上式得：\(s=\frac{A_{sv}}{1.036}=97mm^2,取s=100mm^2\)

综上,箍筋配置如下:选用Ⅰ级钢筋2Φ8,箍筋间距s=100mm。

4 小结

根据上述方法设计出的龙门吊轨道基础梁,经过半年多的运行,证明其强度和变形等均能满足实际要求,车站顶板的变形量也在规定范围之内。计算表明:在轮压作用下,基底压力是以轨道轮作用点为中心,沿四周逐渐降低的。轨道轮轮压的应力扩散半径小于龙门吊相邻两个轨道轮间的距离,轨道轮之间的应力叠加作用可忽略不计。轮压引起的基础变形很小,不会对龙门吊的运行造成不利影响。

[/reply]

文章来源：

《地铁车站顶部龙门吊轨道基础设计计算》张厚美 赖兆武 张良辉( 广州市盾建地下工程有限公司? 广州? 510030)