切基线法、弦基线法测设复曲线（含有缓和曲线的复曲线）

复曲线是由两个或两个以上半径不同、转向相同的圆曲线相连接或插入缓和曲线组成。复曲线在铁路的新线设计中很少采用，一般应用在地形复杂的地区、矿区、工业厂区或路线转向处。按其连接方式的不同，可分为三种形式:无缓和曲线的复曲线、有缓和曲线的复曲线和两端有缓和曲线、中间也有缓和曲线的组合形式。󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄤󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

一、不设缓和曲线的复曲线

该种复曲线一般仅由两个不同半径的同向圆曲线相互衔接而成。在测设时,必须先定出其中一个圆曲线的半径,该曲线称为“主曲线”,另一个圆曲线称为“副曲线”。副曲线的半径则是通过主曲线半径和测量的有关数据求得。

1.切基线法测设复曲线

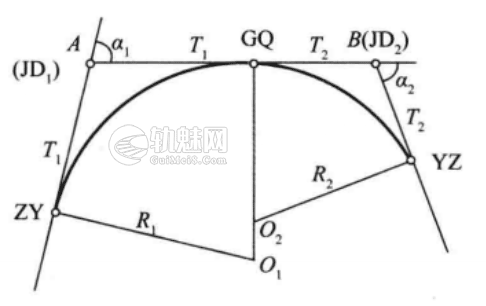
图1 切基线法测设复曲线

切基线法测设复曲线实际上是虚交切基线，只不过是两个圆曲线的半径不相等。如图 1所示,主、副曲线的交点为\(A\),\(B\)两曲线相接于公切点\(GQ\)点。将经纬仪分别安置于\(A,B\)两点,测算出转角\(a_1,a_2\)用测距仪或钢尺往返丈量得到A,B两点的距离\(\overline{AB}\),在选定主曲线的半径\(R\)后,即可按以下步骤计算副曲线的半径\(R_2\)。及测设元素:

(1)根据主曲线的转角\(a_1\)和半径R计算主曲线的测设元素\(T_1,L_1,E_1,D_1\)。󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄤󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

(2)根据基线\(AB\)的长度\(\overline{AB}\)和主曲线切线长\(T_1\)，计算副曲线的切线长\(T_2\):󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄤󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

$$T_2=\overline{AB}-T_1$$

(3)根据副曲线的转角\(a_2\)和切线长\(T_2\)。计算副曲线半径\(R_2\):󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄤󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

$$R_2=\frac{T_2}{\tan\frac{a_2}{2}}（计算至里面）$$󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄤󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

(4)根据副曲线的转角\(a_2\)和半径\(R_2\)计算副曲线的测设元素\(,L_2,E_2,D_2\)。󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄤󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

(5)主点里程计算采用前述方法。󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄤󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

测设曲线时,由A沿切线方向向后量\(T_1\),得ZY点;沿AB方向向前量\(T_1\)，得\(GQ\)点;由B点沿切线方向向前量\(T_2\)。得YZ点。曲线的详细测设仍可用前述的有关方法󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄤󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

2.弦基线法测设复曲线

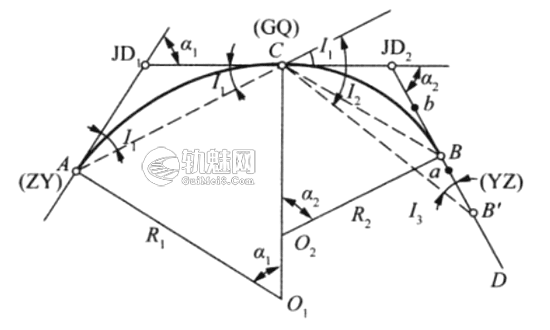
图2 弦基线法测设复曲线

图2所示是利用弦基线法测设复曲线的示意图,设定A,C分别为曲线的起点和公切点，目的是确定曲线的终点B。具体测设方法如下:

(1)在A点安置仪器，观测弦切角\(I_1\)根据同弧段两端弦切角相等的原理，则得主曲线的转角为\(a_1=2I_1\)。󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄤󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

(2)设B’点为曲线终点B的初测位置,在B’点安置仪器观测出弦切角\(I_3\),同时在切线上B点的估计位置前后打下骑马桩a ,b。󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄤󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

(3)在C点安置仪器,观测出\(I_2\)。由图可知,复曲线的转角\(a_2=I_2-I_1+I_3\) 。旋转照准部照准A点,将水平度盘读数配置为0°00’00″后倒镜,顺时针拨水平角\((a_1+a_2)/2=(I_1+I_2+I_3)/2\) ,此时,望远镜的视线方向即为弦CB的方向,交骑马桩a,b的连线于B点，即确定了曲线的终点。󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄤󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

(4)用测距仪(全站仪)或钢尺往返丈量得到AC和CB的长度\(\overline{AC}\),\(\overline{CB}\),并由此计算主、副曲线的半径R₁,R₂得:

$$\left.\begin{matrix}
R_1=\frac{\overline{AC}}{2\sin \frac{a_1}{2}}\\
R_2=\frac{\overline{CB}}{2\sin \frac{a_2}{2}}
\end{matrix}\right\}$$

(5)由求得的主,副曲线半径和测算的转角分别计算主、副曲线的测设元素,然后仍按前述方法计算主点里程并进行测设。[reply]󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄤󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

二、设置有缓和曲线的复曲线

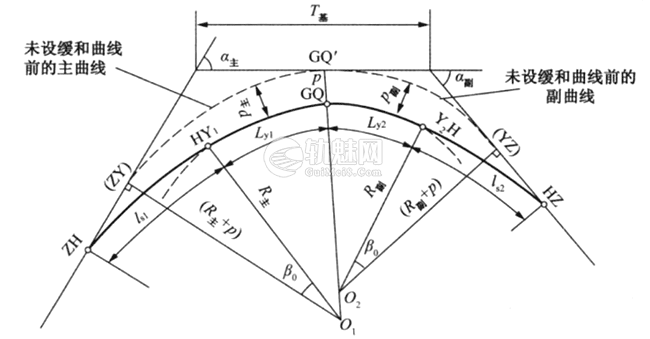
图3 两边皆设缓和曲线的复曲线

1.中间不设缓和曲线而两边皆设缓和曲线的复曲线

如图3所示,设主,副曲线两端分别设有两段缓和曲线,其缓和曲线长分别为\(l_{s1}，l_{s2}\),。为使两不同半径的圆曲线在原公切点(GQ)直接衔接,两缓和曲线的内移值必须相等,即:\(p_主=p_副=p\) 。由前述式(7-28)及式(7-37)有:󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄤󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

$$\left.\begin{matrix}
c_1=R_主\cdot l_{s1}=R_主\cdot\sqrt{24R_主p}\\
c_2=R_副\cdot l_{s2}=R_副\cdot\sqrt{24R_副p}
\end{matrix}\right\}$$

如果R_主>R_副,则C₁>C₂。因此在选择缓和曲线长度时,必须使\(c_2=0.035v^3\) 。对于已选定的l_s2 ,可得:

$$l_{s2}=l_{s1}\cdot\sqrt{\frac{R_副}{R_主}}$$󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄤󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

另外,图3中有如下的关系式:

$$T_基=(R_主+p)\cdot \tan\frac{a_主}{2}+(R_副+p)\cdot \tan\frac{a_副}{2}$$󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄤󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

测设时,通过测得数据\(a_主\)，\(a_副\)和\(T_基\),以及根据要求拟定的数据\(R_主,l_{s1}\),采用上式反算\(a_副\)，其中：\(p=p_主=\frac{l^2_{s1}}{24R_主}\);采用\(l_{s2}=l_{s1}\cdot \sqrt{\frac{R_副}{R_主}}\)反算副曲线缓和段长度\(l_{s2}\),_。

主、副曲线的半径,转角和缓和段长度均已设定的情况下,可按前述的方法进行测设元素及主点里程的计算。󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄤󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

2.中间设置有缓和曲线的复曲线

中间设置有缓和曲线的复曲线是指复曲线的两圆曲线间有缓和曲线段衔接过渡的曲线形式。一般在实地地形条件限制下，选定的主,副曲线半径相差悬殊超过1.5倍时采用。在实际工程测量中,应尽量避免采用这种曲线,故在此不作介绍。

[/reply]

文章来源：

来自 赵树青，孟凡涛主编. 《工程测量技术》[M]. 2015󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄤󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮