轨道竖向静力计算公式

1 基本假设

①假设列车运行时,车轮荷载在轨道各部件中所引起的应力、应变,与量值相当的静荷载所引起的应力、应变相等,即车轮荷载具有准静态性质。

②以速度系数、横向水平力系数、偏载系数分别反映车轮垂直动荷载、横向水平力和垂直力偏心、曲线内外轨偏载的影响。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

③假设轨道及基础均处于线弹性范围,列车轮系作用下轨道各部件的应力、应变,等于各单独车轮作用下的应力、应变之代数和。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

④视钢轨为连续弹性基础上的等截面无限长梁,梁的基础反力与各自弹性下沉之间成线性关系。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

⑤不计钢轨、扣件及轨枕本身的自重。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

2 计算模型

依照弹性基础上无限长梁支承方式的不同,轨道结构竖向受力的静力计算模型分为弹性点支承梁模型和连续弹性基础梁模型,分别如图1( a) ,( b)所示。

图1 轨道结构竖向静力计算支承梁模型

1)弹性点支承梁模型

将对钢轨的支承按一定间隔离散至各个轨枕上,每个轨枕处简化为对钢轨的弹性点支承，着重反映的是轨道系统的最基本,总体上的特征。由于该模型中对钢轨的支承是不连续的，因此可采用差分法或有限元法进行求解分析。

2)连续弹性基础梁模型

连续弹性基础梁模型是把钢轨视为一根支承在连续弹性基础上的无限长梁进行轨道静力分析。它将轨枕对钢轨的支承视为连续支承,其支承刚度为钢轨基础弹性模量u。用该模型可以求得精确严密的解析解,方法简便直观,更符合实际情况。目前世界各国和我国铁道总公司标准《铁路轨道设计规范》(TB 10082—2005)均采用连续弹性基础梁模型,因此本章着重介绍这种方法。

3 计算参数

采用连续基础梁模型进行计算时,需先确定如下一些计算参数:

1)钢轨抗弯刚度EI

EI为钢轨钢的弹性模量E和钢轨截面对其水平中性轴的惯性矩I的乘积。E值一般取为2.1 ×10⁵MPa。I 可根据不同的钢轨类型及其相应的垂直磨耗程度从表1中查得。

表1 各种类型钢轨截面惯性矩与截面系数

2)钢轨支座刚度D

D表示钢轨支座的弹性特征,是用来表征钢轨扣件和枕下基础的等效刚度。它是使钢轨支点顶面产生单位下沉时施加于支点顶面上的钢轨压力,单位为N/mm。

D的表达式为（公式1）:

$$D=\frac{R}{y_p}$$

式中

R——作用在支座上的钢轨压力,N;󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

y_p——钢轨支座下沉量, mm。

图2 钢轨支点刚度

如图2所示,钢轨支座刚度D分别由橡胶垫板,轨枕及道床和路基的支承刚度组成。混凝土轨枕刚度很大,在实际分析中认为其不可压缩,即认为混凝土轨枕的支承刚度D_s无限大，所以,当轨枕为混凝土材质时,钢轨支点刚度D仅由橡胶垫板D_p、道床和路基D_b两部分的支承刚度组成,模拟成两个串联的弹簧组合,因此,钢轨支点刚度D可表示为（公式2）:

$$\frac{1}{D}=\frac{1}{D_p}+\frac{1}{D_b}$$

D值随材料的性质、路基和道床密度及气候的影响而变化。根据我国的测定数据,混凝土轨枕轨道的D值见表2所示。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

表2 混凝土轨枕轨道的D值

3)道床系数C

道床系数C用来表征道床及路基的弹性特征,定义为使道床顶面产生单位下沉所需要施加于道床顶面单位面积上的压力,量纲为(力/长度³),可通过(公式5)计算（公式3）:

$$C=\frac{p}{y_o}$$

式中

C——道床系数, MPa/ cm;󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

p———作用于道床顶面单位面积上的压力, MPa ;󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

y_o——轨枕底面的平均下沉量, cm。

道床系数C的取值见表3。

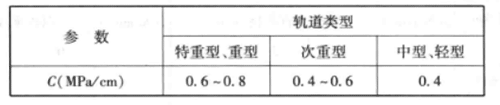
表3 道床系数值

4)钢轨基础弹性模量u

钢轨基础弹性模量u用来表征钢轨基础的弹性特征,定义为单位长度的钢轨基础产生单位下沉所需的施加在钢轨基础上的分布力,量纲为(力/长度³),可通过式计算(公式4):

$$u=\frac{D}{a}$$

式中

a——轨枕间距, cm;

u——钢轨基础弹性模量,kN/cm²。

其中,C、D、u3个弹性特征参数数值是离散性很大的随机变量,如果选择不当,计算结果会引起很大的误差。因此,尽可能采用实测数据。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

5)刚比系数h

k是指钢轨基础弹性模量与钢轨抗弯刚度的比值,是轨道系统的特征参数,可用公式5计算。对于混凝土轨枕，k的取值可参见表4。轨道的所有力学参数及相互间的关系均反映在h中,任何轨道参数的改变都会影响k,而k的改变又会影响轨道的内力分布和部件的内力分配。

公式5：

$$k=\sqrt[4]{\frac{u}{4EI_x}}=\sqrt[4]{\frac{D}{4EI_xa}}=\sqrt[4]{\frac{1}{4EI_xa}}\times \sqrt[4]{\frac{1}{\sum \frac{1}{D_i}}} $$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

表4 混凝土轨枕线路的u、k值

4 单个轮对作用下的方程及解

1)文克尔假定

假设钢轨上作用有集中荷载P,以y(x)表示钢轨的挠度曲线,以向下为正。以q(x)表示基础对钢轨的分布反力,以向上为正。为建立基础梁微分方程,文克尔提出了如下假设（公式6）:

$$q(x) = uy(x)$$

即假设x坐标处的基础反力与x处的钢轨位移成正比。这相当于假设基础是由连续排列,但相互独立的线性弹簧所组成,即每个弹簧的变形仅决定于作用在其上的力,而与相邻弹簧的变形无关。由于实际的轨枕支承是有一定间距的,且碎石道床并不是连续介质,一根轨枕的少许下沉,对相邻轨枕影响较小,所以文克尔假设对于分析轨道问题来说还是比较适合的。大量实验证明,用这种模型计算的结果是能够满足一般分析精度要求的。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

2)连续基础梁微分方程的建立及求解

(1)连续基础梁微分方程

根据图1(b)的计算模型,钢轨作为连续弹性基础上的无限长梁,在集中荷载Р的作用下产生了挠曲,如图3所示。产生的挠曲曲线用y(x)(设向下为正方向)表示,轨下基础的分布反力q(x)。
设Р力在坐标原点Q上,挠度向下为正;截面左面的弯矩M ,顺时针为正;剪力向上为正;其弹性曲线的方程可表示为y=y(x)。当变形微小时,由材料力学可知,钢轨各截面的转角θ、弯矩M、剪力Q和基础反力强度q(x)分别为:

图3 钢轨竖向受力及变形

公式7-10：

$$\theta =\frac{dy}{dx}\\M=-EI_x\frac{d^2y}{dx^2}\\Q=\frac{dM}{dx}=-EI_x\frac{d^3y}{dx^3}\\q(x)=\frac{dQ}{dx}=-EI_x\frac{d^4y}{dx^4}$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

式中

M——钢轨弯矩, kN· cm;󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

Q——钢轨剪力, kN;

q(x)——轨下基础分布反力,kN/ cm。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

根据文克尔( Winkler)弹性地基理论假设,轨下的基础反力q与梁的挠曲变形y成正比,即（公式11）:󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

$$q(x) = uy(x)$$

式中u———钢轨基础弹性模量,kN/cm²。

将式(公式11)代入式(公式10),可得（公式13）:󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

$$uy(x)=-EI_x\frac{d^4y}{dx^4}$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

即（公式13）：

$$\frac{d^4y}{dx^4}+\frac{u}{EI_xy(x)}=0$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

式(13)为4阶常系数线性齐次微分方程,令\(k=\sqrt[4]{\frac{u}{4EI_x}}\),其特征方程为（公式14）:󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

$$\lambda ^4+4k^4=0$$

λ对应的4个根如下:

$$\lambda _{1,2}(1\pm i)k \qquad \lambda _{3,4}(-1\pm i)k $$

由以上可知,方程(13)的通解为（公式15）:󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

$$y(x)=C_1e^{kx} \cos kx+C_2e^{kx} \sin kx +C_3 e^{-kx} \cos kx +C_4e^{-kx} \sin kx$$

(2)边界条件

式(15 )中,C₁.C₂.C₃.C₄为积分常数,可以通过如下边界条件确定:

当x→∞时,y =0，C₁=C₂=0;

②荷载作用点处钢轨转角为零,即\(\frac{dy}{dx}=0,C_3=C_4\);󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

③当x=0时,Q =P/2 ,即:󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

$$Q=-EI_x\frac{d^3y}{dx^3}=\frac{P}{2},C_3=C_4=\frac{P}{8EI_xk^3}=\frac{Pk}{2u}$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

(3)微分方程的解

将C₁,C₂.C₃.C₄代入方程(4.15) ,可解得钢轨在车轮集中荷载Р作用下的钢轨挠曲变形方程为（公式16）:

$$y(x)=\frac{Pk}{2u}e^{-kx}(\cos kx+\sin kx)$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

钢轨弯矩方程为（公式17）:

$$M(x)=-EI_x\frac{d^2y}{dx^2}=\frac{P}{4k}e^{-kx}(\cos kx -\sin kx)$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

钢轨作用于轨枕上的力,即枕上压力R(x)可通过轨下基础分布反力q(x)与轨枕间距a的乘积得到,即（公式18）:󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

$$R(x)=a\times q(x)=\frac{Pka}{2}e^{-kx}(\cos kx + \sin kx)$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

以上计算所得的式(16),式(17),式(18)分别对应于钢轨在一个车轮集中荷载作用下的位移y(x)、钢轨弯矩M(x)、枕上压力R(x)的解析,对这3个式子作数学分析可以看出刚比系数k在决定轨道的变形与内力分配方面起着重要作用。弯矩M和枕上压力R的分布,不是由u或EI单独决定的,而是决定于比值u/EI。当k值较大时,基础相对较硬时,则枕上压力R较大,弯矩M较小,且向两侧衰减较快,荷载影响的范围较小;相反,如果钢轨的弯曲刚度E较大,而基础相对较软,则荷载的影响将与上述情况相反。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

通过计算可知,当kx=0(即x=0)时,即在车轮荷载的作用点处,各个解取得最大值;当kx≥5时,轮载的影响已经很小,通常可忽略不计。单个车轮荷载作用下的钢轨挠曲变形曲线，如图4(a). (b)所示。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

图4 单个车轮荷载作用下的钢轨位移及弯矩图

5 群轮荷载作用下的方程及解

由于式(13)为4阶常系数线性齐次微分方程,故在计算多个轮载同时作用于钢轨上时，可采用叠加原理进行求解,如图5所示,具体过程如下:

如图5所示,现要计算钢轨某位置处的受力与变形(假设该位置处为坐标原点,称该截面为计算截面),假定计算轮对3处钢轨的挠曲变形y₀,钢轨弯矩M₀以及枕上压力R₀轮对荷载分别为P₁, P₂,P₃,P₄.P₅,轮对之间距离如图6所示。根据式(16),式(17),式(18 )，分别计算出各个轮对在计算截面处所引起的钢轨挠曲变形y(x),钢轨弯矩M以及枕上压力R(x) ,并将所得结果线性叠加,这样就得到了计算截面处的受力与变形,具体公式如下（公式19）:

$$y_0=\frac{k}{2u}\sum_{i=1}^{n}P_ie^{-kx_i}(\cos kx_i+\sin kx_i)\\M_0=\frac{1}{4k}\sum_{i=1}^{n}P_ie^{-kx_i}(\cos kx_i+\sin kx_i)\\R_0=\frac{ak}{2u}\sum_{i=1}^{n}P_ie^{-kx_i}(\cos kx_i+\sin kx_i)$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄩󠄧󠄞󠄡󠄤󠄞󠄨󠄧󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

式中

P_i——各个车轮荷载;

x_i——各轮位同计算截面的距离。

图5 多个轮载作用下钢轨受力变形示意图

图6 群轮作用下各轮位的计算距离

应该注意的是,相邻车轮对于同一计算截面计算所得结果有正有负,因此,对于多个轮对作用下的钢轨的受力和变形,宜将每个轮对位置处分别作为计算截面进行计算,通过叠加比较找出最不利截面的位置。如图6所示,当有3个轮作用时,需要分别对中间轮为计算轮、第一轮为计算轮不同情况进行计算,找出最不利作用工况。

文章来源：

高亮编著. 《轨道工程》[M]. 2015