既有线路曲线要素的测量与计算

0 引言

铁路建设不仅指新线建设，同时还包括既有线的改建。既有线改建涉及线路控制网的布设以及对曲线要素的评价。在新线中，线路控制网、曲线要素已经布设好和设计好; 要改建既有线，就应该知道改建前既有线的线路要素。由于既有线路肩两边的控制桩变形或不存在，采用以前的控制网已不可靠。因此，应沿线路走向重新布设控制网，采集铁路轨道坐标。

1 建立线路控制网

首先布设既有线线形测量控制网，铁路改建控制网按新线铁路控制网( CPⅠ、CPⅡ) 的形式建网，CPⅢ网沿线路方向布设成导线网; 然后在CPⅢ控制点上采集铁路轨道离散点中心坐标，宜按三级布设，即先建立基础平面控制网( CPⅠ) ，该控制网沿线路走向布设，每4 km 一个点，布设在离线路中线50—500 m 附近，且不易被破坏的范围内。建立完该控制网后布设线路控制网( CPⅡ) ，此控制网在基础平面控制网( CPⅠ) 上沿线路附近布设，控制点边长以400—600 m 为宜，一般选在离线路中线50—100 m。基桩控制网( CPⅢ) 建立的原则: 直线段宜布设在下行线左侧路肩上，曲线部分宜按上、下行线分别设置。

CPⅢ控制点的距离宜在150—200 m。布置在线路两边，该网为导线网，其三级平面控制网示意图如图1 所示。该控制网的精度直接决定了采集线路中线坐标的精度以及计算既有线线形要素的精度。

2 线路中线点坐标的采集及其精度

由上一节可知已在既有线线路方向上布置了CPⅢ。然而既有线经多次提速后，列车行车速度已经很高，在既有线上测量，安全问题更为突出，特别是测量线路中线坐标更加危险。为了保证安全和提高测量速度与精度，采用在CPⅢ上设站任意置镜极坐标法测量左轨坐标，该方法作业时间短，安全系数高。采用极坐标测量线路左轨坐标时，应根据行车密度和线路线形而定。理论上在既有线上测的点密度越大，就越能反映既有线的实际线形，但是在实际作业中，要求效率高并且危险系数小，因此在作业中必须考虑采集点的密度，采集密度遵循的原则为既能反映既有线线形，又能提高作业效率和安全系数。

建议在直线段每隔20 m 采集一个点; 在曲线段，当曲线较短时，建议以曲线长的十分之一为采样间隔，不一定采用统一的长度采集。
由极坐标公式可知，既有线左轨处任意一点处的坐标可以表示为:

x_i = X_cpⅢ+ S* cos( A + α)          （1）

y_i = Y_cpⅢ+ S* sin( A + α)          （1）

式中，角A 为设站点到后视点的方位角。
由误差传播定律可知，既有线左轨处任意一点处的坐标中误差可以表示为:

m²_xi = m²_XCPⅢ+m²_S×cos²(A+α)+S²×sin²(A+α)×m²_(A+α)×1 /ρ²       （2）

m²_yi = m²_YCPⅢ+m²_S×sin²(A+α)+S²×cos²(A+α)×m²_(A+α)×1 /ρ²       （2）

设测角中误差为m_α‘; 测距中误差为ms( mm) 。若不顾及控制点本身误差、仪器对中、整平误差，式( 2) 可以表示为:

m²_xi =m²_S× cos²( α)+S²×sin²( α)×m²_α×1/ρ²      （3）

m²_yi =m²_S× sin²( α)+S²×cos²( α)×m²_α×1/ρ²       （3）

则该点的点位中误差可以表示为:

m²_i= m²_xi+m²_yi                                （4）

若以Leica TCA 2003 全站仪施测，该全站仪的测角精度为0．5″，测距精度为1 mm+1 ppm，由式( 3) 、式( 4) 可得出不同角度、不同距离时的点位中误差，由式( 3) 知x 和y中的第二项可以省略不计，由此得到该点的点位中误差只与距离有关。在测量时，最远的距离不会大于200 m，因此最大的点位中误差为±1．44 mm。在实际测量中距离不可能超过200 m，因此曲线上的点位中误差比±1．44 mm要小。通过上面分析得知，采用在CPⅢ上设站任意置镜极坐标法测量左轨坐标是可行的，为下面计算既有线线路要素提供了精度保障。

3 既有线线路要素计算原理

缓和曲线的两端为两条直线，由数学公式可知，直线方程可以写成:

y = kx + b                             （5）

对于直线来说，观测了一组数据，记为Z₁( x₁，y₁) 、Z₂( x₂，y₂) …Z_n( x_n，y_n) 。可以由这组数据的其中两个数据求出该直线方程，但是既有线路运行多年，线路已经变形，单凭直线段上的两三个点很难反映直线段的线形。
为了能够比较准确地反映直线段的真实线形，将上面观测的数据代入上式，并写成矩阵的形式: （6）

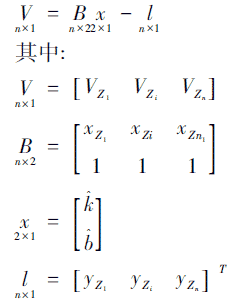
按最小二乘原理求解有:

x=( B^TPB)^-1B^TPl                             （8）

采用上面的方法可以求出缓和曲线两端的直线方程式，根据两条直线的斜率，依据下式可以求出该条缓和曲线的转角和交点坐标。

α = arctank₁－arctank_{2                            （9）}

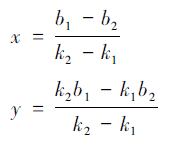
其中: arctank1

为其中一条直线在线路坐标系下的方位角，arctank₂为另一条直线在线路坐标系下的方位角。b₁、b₂为其对应直线的切距。

圆曲线的方程可以表示为:

x²+ y²+Ax+By+C=0                            （11）

则圆心与半径可以由圆曲线的系数表示为:（12）

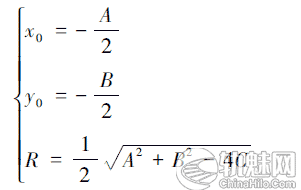
对于圆曲线来说，观测了一组数据，记为Y₁( x₁，y₁) 、Y₂( x₂，y₂) …Y_n( x_n，y_n) 。可以由这组数据其中的3 个数据求出该圆曲线的要素。为了能够比较准确地反映圆曲线的真实线形，将上面观测的数据代入式 ，并写成矩阵的形式:（13）

按最小二乘原理以及式( 8) 可求出圆心坐标和圆的半径。

参照文献1，缓和曲线的参数方程可以表示为:（14）

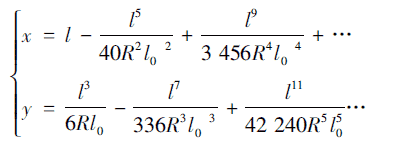
其中: Ｒ为圆曲线半径，单位为m; l_o为缓和曲线段长度，单位为m; l 为缓和曲线上的点到直缓点的长度，单位为m。

x、y 表示缓和曲线上任意点i 在以直缓点为坐标原点，以直缓点的切线方向为x 轴，与x 轴相垂直且方向指向曲线内侧为y 轴( 曲线元的曲率中心一侧) 的局部坐标系的坐标，C=Ｒl₀。后面未加以说明都是指这种局部坐标系。

缓和曲线的局部坐标y 也可以表示为:（15）

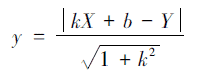
其中: k 为过直缓点切线的斜率; b 为过直缓点切线的切距; X、Y 为缓和曲线上任意一点在线路坐标系下的坐标。

由上式可知，在获得缓和曲线上任一点的线路坐标和过直缓点切线的斜率以及切距的情况下，就可以知道该点在局部坐标系中的纵坐标。

由式( 14) 知道缓和曲线上任一点以及该点的下一点纵坐标可以表示为:（16）

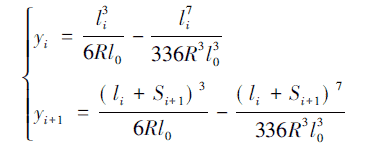
其中: S_i+1为第i点到第i+1点的距离。

由式( 15) 可以求出该点在局部坐标系下的纵坐标，在Ｒ 已经解出的条件下，由式( 16) 可以求出l₀、l_i。

将式( 16) 中的两式整理为:

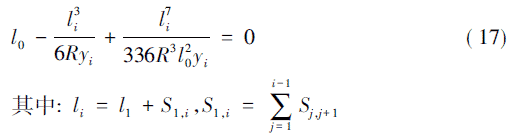
式( 16) 中l₀ =l₀⁰，l_i= l₁⁰初值理论上可以由缓和曲线的前两点确定，但是在既有线上测量时不能保证前两点在缓和曲线上，因此建议采用缓和曲线第四个点以后的点作为初值，将式( 17) 按泰勒公式展开，并略去高次项有:

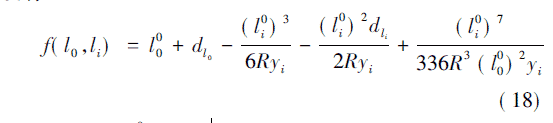
由于l_i=l_i⁰+S_1，j将在缓和曲线上的点代入上式并写成矩阵的形式有:

就缓和曲线观测了一组数据。可以由这组数据其中的两个数据求出缓和曲线长。为了最佳地反映出缓和曲线的真实长度，按最小二乘原理以及式( 8) 得到最佳长度。由于初始的缓和曲线长度是一个近似值，因此采用迭代的方法直到Δl = l_i+1－l_i小于某个数为止。

4 应用实例

基于上述思想，笔者采用c#2003 编制了程序。程序在读取原始数据后，能够计算出既有线线路要素，包括曲线的切线长、转角、内移量、切垂距等。将计算得到的既有线线路要素与设计的既有线线路要素进行比较，比较值见表1。从表1 中得出在线路上采集的点越多就越能反映线形，就圆曲线半径来说，第三条圆曲线上采集的多于第一条圆曲线上的点，第三条计算得到的圆半径与理论的差值为1 mm，完全可以忽略不计。结合表1 可以得出，采用这种方法拟合曲线的实际线形是可靠的。

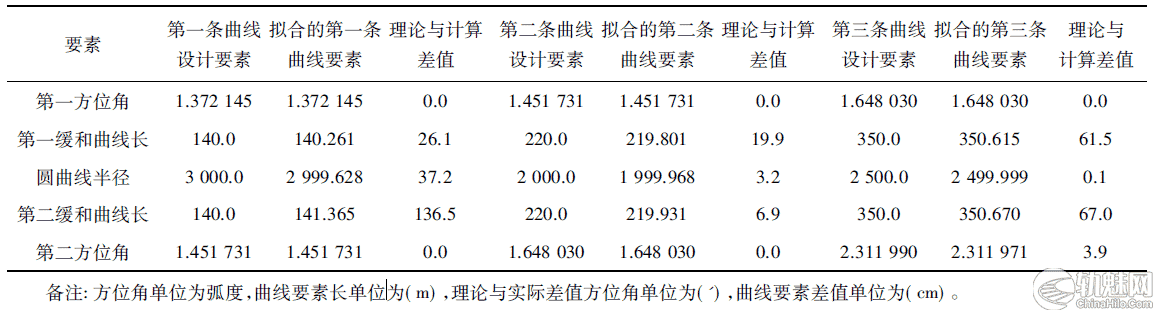
表1 既有线线路要素设计与拟合结果比较表

5 结束语

本文根据既有铁路曲线测量的常用方法，对常规既有铁路曲线测量的方法进行了改进，提出了一种用于计算既有线线路要素的方法。通过对既有线线路要素原理的探讨，并且用实例证明了该方法在理论上是合理的。

该方法能够计算出既有线线路要素，对铁路提速具有一定的实际意义。

文章来源：

《既有线路曲线要素的测量与计算》彭剑秋，申学林，李亮( 自然资源部第六地形测量队，四川成都610500)