超声波探伤中测定缺陷在工件中的具体位置,称为定位。我们常用垂直高度和水平距离的二轴坐标来确定缺陷的位置。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄤󠄤󠄞󠄣󠄦󠄞󠄡󠄢󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
1 垂直法探伤的定位
垂直法探伤定位比较简单,探头波束轴线垂直入射工件,缺陷回波达到最高值时,缺陷的位置就在探头的入射点之下,即缺陷正好位于探头中心轴线上,只要测定缺陷在工件中的深度,就可对缺陷定位。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄤󠄤󠄞󠄣󠄦󠄞󠄡󠄢󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
当探伤仪按声程测距时,仪器基线刻度与声程的比例系数K确定后,若缺陷波前沿所对应的水平刻度值m,则缺陷至探头的距离󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄤󠄤󠄞󠄣󠄦󠄞󠄡󠄢󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
h=Km。
2 斜角法探伤的定位
斜角法探伤时,缺陷的水平位置不在探头入射点的法线上,需要通过三角函数关系来计算缺陷的水平距离和垂直深度。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄤󠄤󠄞󠄣󠄦󠄞󠄡󠄢󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
以横波斜探头探测平面为例:
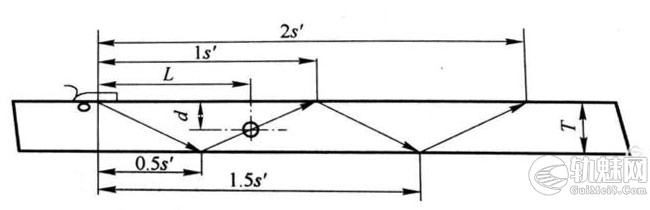
横波折射角为β,即声束轴线与探测面法线的夹角,声束由入射点O倾斜入射到工件下表面所对应探测面上的投影距离为0.5s’,声束又从工件下表面反射到上表面,此时整个投影距离为1s’,此即为声波在工件上探伤所产生的跨距,依此类推,有1.5s’,2s’等。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄤󠄤󠄞󠄣󠄦󠄞󠄡󠄢󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
当声波在0s~0.5s’范围内探测时,称为一次波探测。在0.5s’~1s’范围内探测时,称为二次波探测,显然还应有三次波、四次波探测等,缺陷从探测面上的投影点到探头声束入射点之间的水平距离L称为探头距离,缺陷至探测面的垂直距离h称为缺陷深度。缺陷的位置即由这两个参数确定。由于横波扫描速度可按声程、水平、深度来调节,因此缺陷定位的方法也不一样。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄤󠄤󠄞󠄣󠄦󠄞󠄡󠄢󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
① 按声程调节扫描速度
仪器按声程1:n调节横波扫描速度,缺陷波水平刻度为r。一次波探伤时,缺陷至入射点的声程S=nr,则缺陷在工件中的水平距离L和深度h为󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄤󠄤󠄞󠄣󠄦󠄞󠄡󠄢󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$L=S\sin\beta \qquad h=s\cos\beta $$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄤󠄤󠄞󠄣󠄦󠄞󠄡󠄢󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
二次波探伤时,S=nr(s1+S2),若工件厚度为T,则缺陷在工件中的水平距离L和深度h为:󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄤󠄤󠄞󠄣󠄦󠄞󠄡󠄢󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$L=S\sin\beta \qquad h=2T-S\cos\beta $$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄤󠄤󠄞󠄣󠄦󠄞󠄡󠄢󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
② 按水平调节扫描速度
仪器按水平距离1:n调节横波扫描速度,缺陷波的水平刻度为r,采用K值探头探伤,一次波探伤时,缺陷在工件中的水平距离L和深度h为:
$$L=n\pi \qquad h=\frac{L}{K}=\frac{L}{tan\beta }$$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄤󠄤󠄞󠄣󠄦󠄞󠄡󠄢󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
二次波探伤时,缺陷在工件中的水平距离L和深度h为:󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄤󠄤󠄞󠄣󠄦󠄞󠄡󠄢󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$L=n\pi \qquad d=2T-\frac{L}{K}$$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄤󠄤󠄞󠄣󠄦󠄞󠄡󠄢󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
文章来源:
原文名称:超声波探伤中缺陷的定位󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄤󠄤󠄞󠄣󠄦󠄞󠄡󠄢󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
原文地址:https://www.meipian.cn/1508s98e󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄤󠄤󠄞󠄣󠄦󠄞󠄡󠄢󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮




