轨道的状态直接决定轨道—车辆系统运行的安全性和舒适性。随着列车速度的提高,对轨道的平顺性提出了更高的要求。为了提高维修效率和节约维修成本,许多发达国家相继进行了轨道维修体制的改革,用状态修替换传统的周期性维修模式。实施状态修的核心是利用大量的检测数据对轨道的状态进行科学合理的评判,动态掌握和预测轨道的发展趋势。目前,国内外对轨道不平顺的管理主要采用幅值管理和区段管理。此外,有些国家还利用车辆动态响应(包括轴箱加速度、车体加速度或轮轨作用力)对轨道状态进行辅助评判[1]。
轨道不平顺包含不同波长成分的不平顺,其中波长为0.01~120m 的不平顺比较常见。轨道不平顺按其波长可分为短波、中波和长波不平顺3类。波长1m 以下短波不平顺的幅值很小,多在0.1~2.0mm 范围内,主要是由钢轨接头焊缝、道岔以及钢轨不均匀磨耗、波浪和波纹磨耗等因素造成的。由于轨道几何检测系统能够检测到的轨道不平顺波长通常在2~150m之间,难以评判短波不平顺对高速铁路轨道-车辆系统运行安全性和舒适性的影响,为此需要研究其他辅助评判手段。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
轴箱直接与轮对相连,轨道不平顺产生的振动通过轮对直接传递到轴箱上,从而引起轴箱的垂向和横向振动。如果将轮对近似地看成是刚性结构,则轴箱的振动加速度可直接反映由轨道短波不平顺所引起的外界激扰力对车辆动力学的影响。因此,许多学者采用轴箱垂向振动加速度辅助评判轨道短波不平顺对车辆动力学性能的影响。Grassie[2]总结了采用轴箱垂向振动加速度评判轨道短波不平顺状态的优点,包括轴箱垂向振动加速度的检测设备易于安装和维护,而且与轮轨力检测系统相比,经济实用,可安装在普通的营运车辆上。Caprioli等[3]利用小波从轴箱垂向振动加速度中提取轨道短波不平顺的频率特征。文献[4—6]利用轴箱垂向振动加速度诊断波磨。文献[7—8]利用轴箱垂向振动加速度诊断轨道短波不平顺,并建议针对不同类型的轨道短波不平顺病害,应采用不同的带通滤波频率处理轴箱垂向振动加速度信号。Hirofumi等[9]分析了轴箱垂向振动加速度的方差与车轮负荷波动的关系。Eric等[10]采用轴箱垂向振动加速度的功率谱表示轨道表面的粗糙度。Remennikov等[11]利用轴箱垂向振动加速度估计轮轨力。Molodova等[12]利用有限元模型分析轨道短波不平顺与轴箱垂向振动加速度的关系。Molodova等[13]利用尺度平均小波功率(Scaleaveragedwaveletpower,Sawp)表征轨道扁疤的大小。俞峰等[14]利用轴箱垂向振动加速度的变化反推道床刚度的变化。康熊等[15]基于共振解调,提出了利用轴箱垂向振动加速度评判高速铁路焊接接头状态的评判方法和指标。
由于轴箱的振动加速度是轮轨动态耦合作用的结果,而且呈现高频和高度非线性的特性。因此除了轨道短波不平顺外,车轮及钢轨踏面的形状和材料、车辆悬挂参数、轮轨接触面粗糙度、速度传感器安装位置等都对轴箱垂向振动加速度有很大影响。因此直接利用轴箱垂向振动加速度幅值进行评判,会出现评判结果随机性大和阈值难以确定的难题。对此,文献[4,7,9]提出利用轴箱垂向振动加速度的有效值,而文献[13]采用Sawp定量描述轨道短波不平顺病害的大小,但这2个特征量的计算均需要预先对轴箱垂向振动加速度进行分段。然而,由不合适的分段得到的特征量可能会降低轨道短波不平顺的严重程度。本文从能量的角度刻画轮轨冲击所引起轴箱垂向振动加速度的高频特性,并提出采用轨道冲击指数(Trackimpactindex,TⅡ)评判轨道的短波不平顺状态。
1 利用轴箱垂向振动加速度评判轨道短波不平顺状态的方法
安装在高速综合检测车上的车辆动态响应检测系统可同时采集轴箱、构架和车体的垂向振动加速度,采样频率为2000hz。利用同步信息传输技术从综合系统获得速度和里程信息,然后根据车辆的长度和传感器安装位置对里程进行校正。实测轴箱垂向振动加速度的波形如图1所示。从图1可以看出,当车辆通过轨道某些不良部位时,会产生较大的冲击振动;图中轴箱的垂向振动加速度大于20m·s-1的部位是钢轨焊接接头区。
由于轴箱的垂向振动加速度是高频信号,直接利用它的幅值评判轨道的短波不平顺状态难免会碰到随机性大的问题,即在轨道没有经过任何维修的情况下,上次检测到的轴箱垂向振动加速度超限现象可能会突然消失。从物理的意义上说,冲击信号具有随机性,但冲击能量基本不变。基于此原理,本文提出从能量的角度刻画轮轨冲击所引起轴箱振动加速度的高频特性,利用轴箱垂向振动加速度的移动有效值信号代替原来的波形信号,用于评判轨道的短波不平顺状态。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
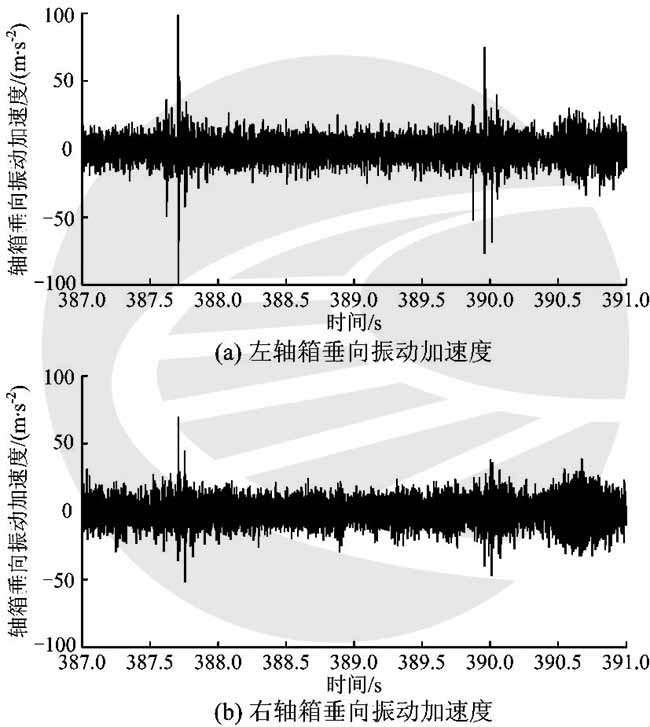
图1 实测轴箱垂向振动加速度波形
记滤波后的轴箱垂向振动加速度波形信号的集合为{Xi|i=1,2,…,N},N 为轴箱垂向振动加速度波形信号的个数,则轴箱垂向振动加速度的移动有效值的集合可记为{Sγ |γ=1,2,…,N-K+1},其中
$$S_\gamma =\sqrt{\sum_{i=\gamma}^{\gamma +K-1} x^2_i/K} \qquad (1)$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式中:K 为向前加窗的窗长。
与轴箱垂向振动加速度波形信号相反,对应的移动有效值是低频信号。从数学的角度看,计算移动有效值信号的过程就是对信号进行光滑处理的过程。由于低频信号比高频信号稳定,因此前后2次检测得到的轴箱垂向振动加速度的移动有效值基本一致,不会出现随机性问题。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
车轮及钢轨踏面的形状和材料、车辆悬挂参数、轮轨接触面粗糙度、速度传感器的安装位置等对轴箱垂向振动加速度影响大的直接体现就是,轴箱垂向振动加速度的移动有效值的平均值会随这些参数的变化而变化。由此提出采用轨道冲击指数对其移动有效值进行规一化处理,据此评判轨道的短波不平顺状态。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
定义TⅡ为轴箱垂向振动加速度的移动有效值与其平均值的比值,即利用轴箱垂向振动加速度移动有效值的平均值\(\overline{S}\)对移动有效值进行归一化处理可得到TⅡ,其表达式为
$$T_Ⅱ=\frac{S_\gamma }{\overline{S} } \qquad (2)$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式中:TⅡ为轨道冲击指数;Sγ为测点γ处轴箱垂向振动加速度的移动有效值;\(\overline{S}\)为轴箱垂向振动加速度移动有效值的平均值。
\(\overline{S}\)的计算过程如下:󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(1)对实测的各测点处轴箱垂向振动加速度进行带通滤波,带通滤波的频率一般取为[10,500]Hz;󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(2)计算滤波后各测点处轴箱垂向振动加速度的移动有效值Sγ;
(3)将轨道划分成单元,单元长度一般取为50m;󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(4)计算各单元移动有效值的最大值,记为单元有效值;󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(5)计算全部相同速度等级线路的单元有效值的平均值,即为标定参数\(\overline{S}\)。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
利用轨道冲击指数评判轨道的短波不平顺状态分2个阶段完成:第1阶段,根据递推关系计算轴箱垂向振动加速度的移动有效值;第2阶段,计算轨道冲击指数,并据此进行评判。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
评判的详细过程具体描述如下:
(1)对实测的各测点处轴箱垂向振动加速度进行带通滤波,带通滤波的频率一般取为[10,500]Hz;󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(2)计算滤波后各测点处轴箱垂向振动加速度的移动有效值;󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(3)计算各测点处的轨道冲击指数;󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(4)将轨道划分成单元,单元长度一般取为50m;󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(5)提取各单元中轨道冲击指数TⅡ的最大值,记为\(T^{max}_{Ⅱ}\) ,同时记录\(T^{max}_{Ⅱ}\)对应点的里程信息;
(6)结合阈值评判轨道的短波不平顺状态,即若某测点处的\(T^{max}_{Ⅱ}\)大于阈值,则判断轨道在该测点处存在状态不良的短波不平顺。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
与简单地利用轴箱垂向加速度的幅值评判轨道短波不平顺状态的方法相比,利用轨道冲击指数评判轨道的短波不平顺状态,不但可以有效避免随机性的影响,而且易于确定评判的阈值。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
首先,关于避免随机性影响的问题,是通过计算轴箱垂向振动加速度的移动有效值,实现将高频问题转换成低频问题,从而大大减少了检测数据分析结果的随机性;其次,关于评判阈值的确定,利用轴箱垂向振动加速度移动有效值的平均值\(\overline{S}\)对移动有效值进行归一化处理,可以得到轨道冲击指数TⅡ,而且归一化处理后评判指标的分布特性相同,再利用其分布规律自然较容易确定评判阈值(根据对大量测试数据的计算分析,作者对阈值取6.0)。
2 实例分析
利用本文方法对高速综合检测列车的轴箱垂向振动加速度进行分析,诊断轨道的短波不平顺状态,并通过与轮轨力的检测结果对比分析,以验证用本文评判方法所得到的诊断结果是正确的。另外,通过用同一线路区段不同检测速度级的检测数据多次试验,进一步验证本文评判方法的稳定性。实测经过某路段时轴箱垂向振动加速度原始波形及计算得到的轨道冲击指数如图2所示。由图2(a)可以看出,当综合检测列车以360km·h-1的速度通过K1129处时的轨道冲击指数为10.9,远远超过了阈值6.0,因此判断该处的轨道状态不良。另外,测得该处的减载率为0.73,接近脱轨限值0.8,也说明该处的轮轨冲击力大,存在较大的跳轨脱轨风险。通过对比轴箱垂向振动加速度的诊断结果和轮轨力的诊断结果,可以验证本文提出的轨道冲击指数评判方法能有效评判状态不良的轨道短波不平顺。此外,从图2 (b)还可以看出,虽然在K1129处轴箱垂向振动加速度的幅值较大,但与其他各处的幅值相比,差别并不是特别明显,这说明直接利用轴箱垂向振动加速度的幅值较难诊断该处轨道的不良状态。
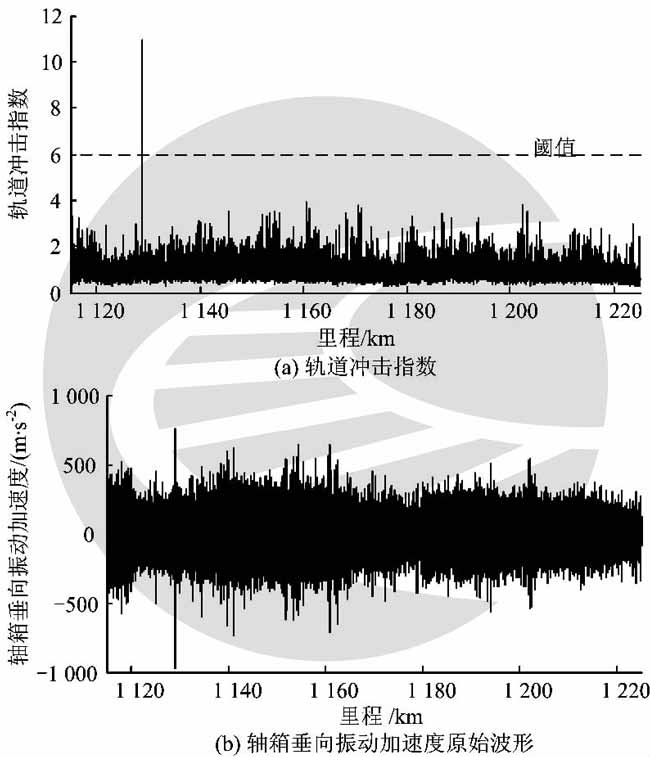
图2 轴箱垂向振动加速度原始波形及对应的轨道冲击
放大K1129超限处邻近范围内的轴箱垂向振动加速度原始波形和对应的轨道冲击指数,如图3所示。由图3可以看出,当轨道存在短波不平顺状态不良时,轮轨之间会发生大的冲击,轴箱的垂向振动加速度呈现先增大然后衰减的过程,虽然不一定会出现特别大的幅值,但积累的冲击能量大。由于轨道冲击指数能够从能量的角度刻画轴箱垂向振动加速度的特性,因此,利用轨道冲击指数能更有效地诊断轨道的短波不平顺病害。
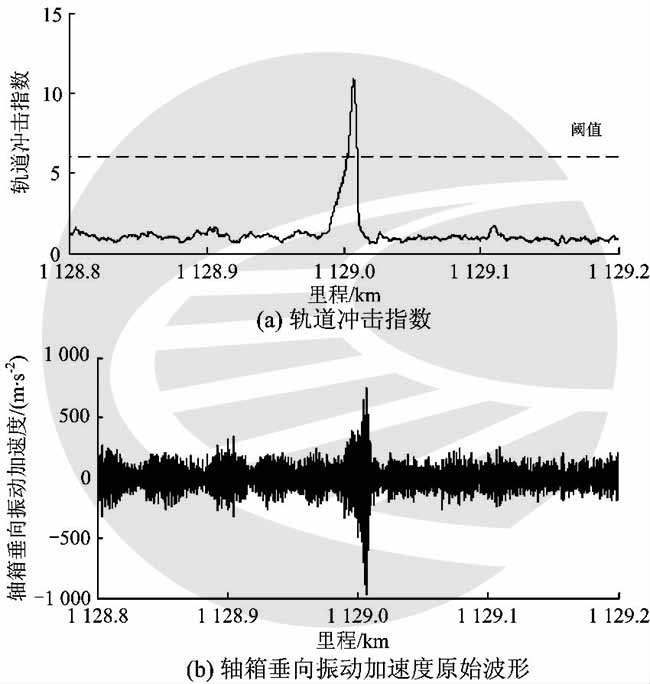
图3 K1129附近的轴箱垂向振动加速度波形及对应的轨
综合检测列车2次以350和2次以360km·h-1的速度多次通过K1129处时轴箱垂向振动加速度的移动有效值比较如图4所示。由图4可以看出,轴箱垂向振动加速度的移动有效值每次都在该处出现大值,而且波形相似。以图4 (a)第1次以360km·h-1的速度通过k1129处时轴箱垂向振动加速度的移动有效值波形为基本波形,其与其他3次通过该处的波形的相关系数分别为0.95,0.95,0.89。由此表明本文提出的评判方法是稳定的,而且具有很好的重复性。
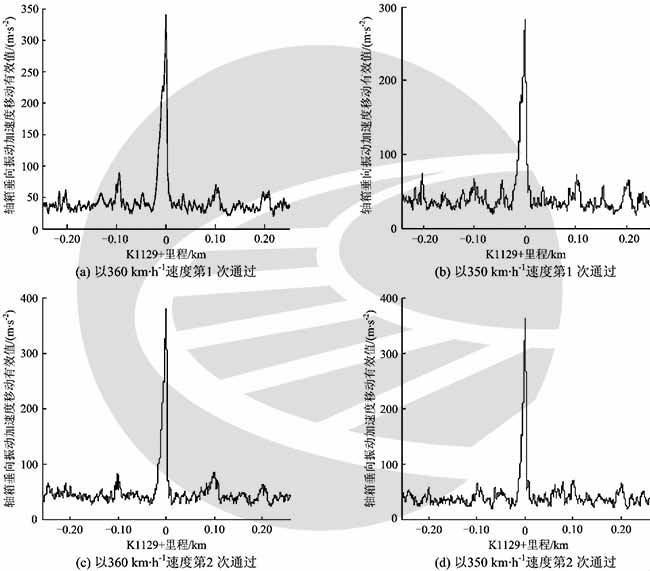
图4 以不同速度多次通过K1129超限处时轴箱垂向振动加速度的移动有效值比较
3 轴箱垂向振动加速度移动有效值的快速计算方法
与传统的有效值计算不同,计算轴箱垂向振动加速度的移动有效值时需要每移动1个点就计算1次移动有效值。因此,采用直接计算轴箱垂向振动加速度移动有效值的传统算法将会碰到计算量太大、难以满足在线分析的要求。作者通过挖掘相邻2个轴箱垂向振动加速度移动有效值的递推关系,提出轴箱垂向振动加速度移动有效值的快速计算方法,从而解决了直接计算碰到的计算量过大问题。
由传统的轴箱垂向振动加速度移动有效值的计算方法(式(1))可知,移动窗内样本点的轴箱垂向振动加速度的平方和为󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$Q^2_\gamma =\sum_{i=\gamma }^{\gamma+K-1} \qquad (3)$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
通过比较相邻的2个轴箱垂向振动加速度平方和可以看出,在计算得到Q^2_\gamma后再计算\(Q^2_{\gamma+1}\)时,对于其中样本点的轴箱垂向振动加速度xk(k=i+1,i+2,…,i+K-1)的平方和计算属于重复计算。于是根据它们的递推关系,设计快速计算轴箱垂向振动加速度移动有效值的算法如下。
(1)以前K个样本点的轴箱垂向振动加速度为第1段,计算该段轴箱垂向振动加速度的平方和\(Q^2_1\)及移动有效值S1,即
$$Q^2_1=\sum_{i=1}^{K} x^2_1 \qquad (4)$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$S_1=\sqrt{\frac{Q^2_1}{K} } \qquad (5)$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(2)在\(Q^2_1\)的基础上递推得到\(Q^2_2\),\(Q^2_3\),…,\(Q^2_{N-k+1}\)以及对应的\(S_\gamma \),即󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$Q^2_\gamma =Q^2_{\gamma -1}+x^2_{\gamma +K-1}-x^2_{\gamma -1} \\ \gamma =2,3,……,N-K+1 \qquad (6)$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$S_\gamma =\sqrt{\frac{Q^2_\gamma }{K} } \qquad (7)$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
通过对比传统的移动有效值计算方法和本文给出的移动有效值快速算法可知,前者的计算量是(N-K+1)× (2K+1),与K 为二次函数关系;而后者的计算量是(N-K+1)×4+2K,与K为线性关系,并且当移动窗的长度K 越长,节省的计算量越大。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
对同一路段分别用传统算法和快速算法计算它们的轴箱垂向振动加速度移动有效值,结果如图5所示。由图5可以看出,用这2种计算方法得到的结果完成相同,说明快速计算方法与传统计算方法的计算精度是一致的。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
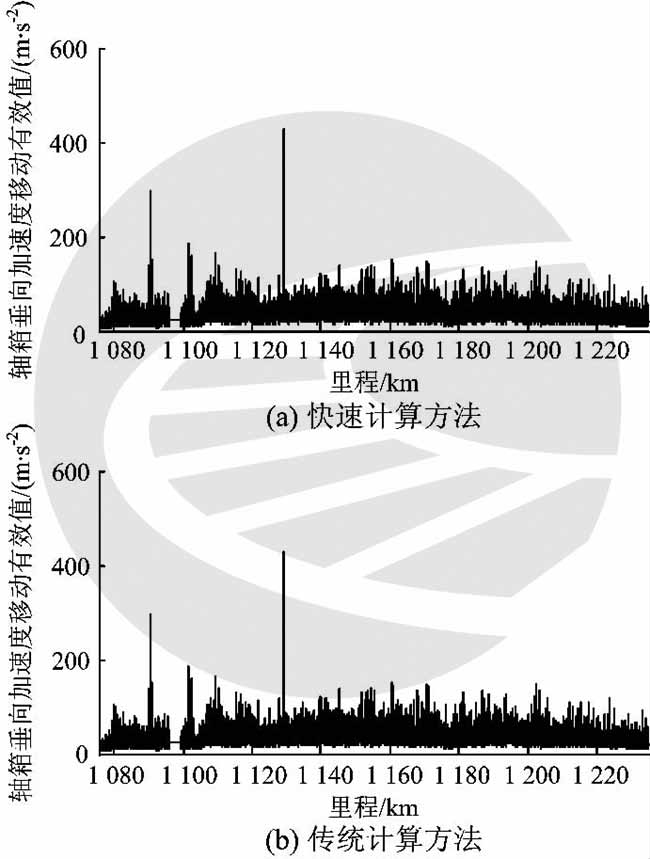
图5 不同方法计算得到的轴箱垂向振动加速度移动有效
再对长度分别为80,100,120,140和160Km的检测路段为例,设定的移动窗长度为60个采样点时,分别利用传统计算方法和快速计算方法计算它们的轴箱垂向振动加速度移动有效值时所需要的时间,见表1。由表1可以看出,快速计算方法所用的计算时间远远少于传统计算方法,仅大概相当于传统计算方法所用时间的1/8,而且随着移动窗长度的增加,快速计算方法节省的计算时间更多。
表1 不同算法计算轴箱垂向振动加速度移动有效值所用计算时间的比较
| 检测路段长度/km | 计算时间/s | |
| 快速算法 | 传统算法 | |
| 80 | 1.9 | 12.6 |
| 100 | 2.1 | 15.6 |
| 120 | 2.4 | 18.7 |
| 140 | 2.6 | 21.7 |
| 160 | 3.2 | 24.5 |
4 轨道冲击指数的归一化效果分析
与直接利用轴箱垂向振动加速度移动有效值的幅值评判轨道短波不平顺状态相比,轨道冲击指数具有规一化的功能。cRH-150C和cRH380B-0301高速综合检测列车相同方向传感器采集并计算得到的左轴箱垂向振动加速度移动有效值如图6所示。

图6 不同车的轴箱垂向振动加速度移动有效值
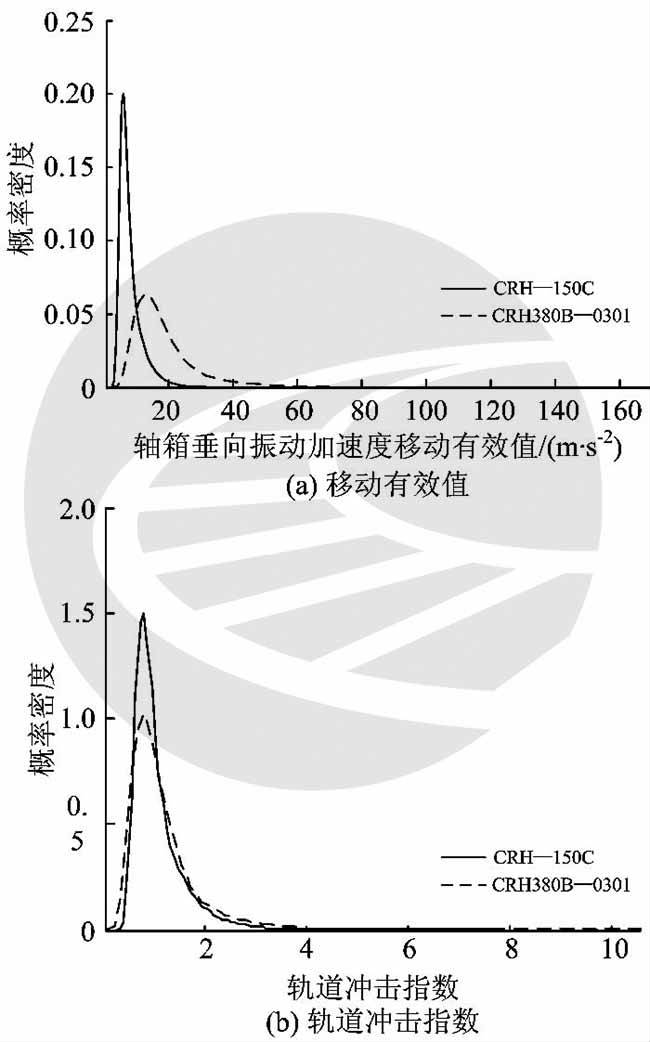
图7 不同车的轴箱垂向振动加速度移动有效值与轨道冲
它们的概率密度和累积概率分布对比分别如图7(a)和图8 (a)所示。从图7 (a)和图8 (a)可以看出,CRH-150C高速综合检测列车的轴箱垂向振动加速度移动有效值主要分布在6m·s-2周围,而CRH380B-0301高速综合检测列车的轴箱垂向振动加速度移动有效值一般分布在13m·s-2 周围。相应的轨道冲击指数的概率密度和累积概率分布对比分别如图7 (b)和图8 (b)所示。从图7(b)和图8 (b)可以看出,不同车的轨道冲击指数的概率密度和累积概率分布曲线基本重合,主要分布在0.8周围。由此可见,对于不同高速车辆的轨道冲击指数,可以近似选择统一的阈值评判轨道短波不平顺的状态。
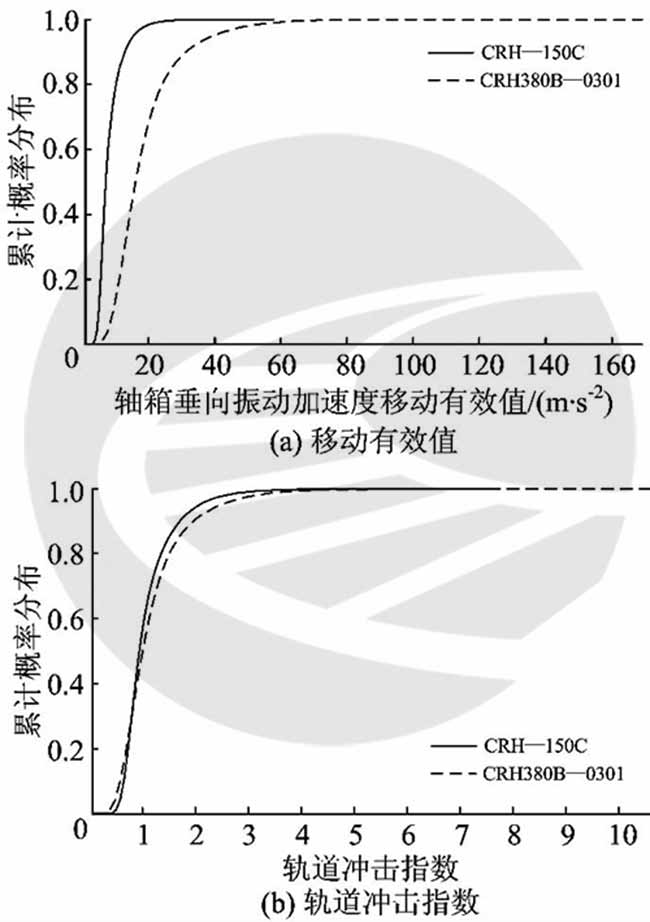
图8 不同车的轴箱垂向振动加速度移动有效值和轨道冲
5 结论
轨道的状态直接决定轨道—车辆系统运行的安全性和舒适性。采用轨道几何检测系统可以有效地对轨道2~150m的中长波不平顺进行管理,但难以评判钢轨焊接接头、磨耗等引起的2m 以下的轨道短波不平顺对高速铁路轨道—车辆系统运行的安全性和舒适性的影响。鉴于轴箱直接与轮对相连,轴箱垂向振动加速度能有效刻画轨道短波不平顺引起轮轨之间高频冲击的特性,故本文提出基于带通滤波后的轴箱垂向振动加速度的轨道冲击指数,用于诊断轨道短波不平顺病害,从而完善了轨道平顺性的评判体系,更好地指导轨道养护维修。直接计算轴箱垂向振动加速度的移动有效值是一个费时费力的工作。本文通过挖掘相邻2个移动有效值的递推关系,提出轴箱垂向振动加速度移动有效值的快速计算方法,有效解决了传统计算方法计算量过大的问题,满足了工程在线应用的要求。
文章来源:
原文名称:评判高铁轨道短波不平顺病害的轨道冲击指数法󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
作者信息:刘金朝,陈东生,赵 钢,刘伶萍,孙善超,郭剑峰,梁志明(中国铁道科学研究院基础设施检测研究所,北京 100081)󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
期刊信息:《中国铁道科学》2016年第4期34-41,共8页󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄩󠄡󠄞󠄡󠄦󠄧󠄞󠄧󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮




