铁路曲线的缓和曲线一般为10m的整倍数,但圆曲线一般不是10m的整倍数,为了提高养护曲线的精度,便于计算以及方便现场对曲线拉绳测量,曲线正矢点按照曲线全长向上规整为10米的整倍数对曲线的正矢点进行分中布设,对于缓和曲线不等长的曲线,应先对圆曲线正矢点进行分中布设,确保曲中位置正确。例如:󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
曲线理论全长为531.135米,长度规整为540米。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
本方法适用于单曲线,需要根据曲线半径、偏角、缓长等曲线要素对曲线全长重新进行检算以确保数据的精确,利用微软的Excel电子表格函数功能可以提高计算效率,具体的曲线分中法正矢计算及布设方法如下:󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
一、通过测量正矢确定曲中及头尾位置
1.在测量现场曲线正矢前,应先将曲线前后直线拨直,把一切不正常弯曲(鹅头)拨入曲线范围以内。
2.在曲线外轨每隔10米用钢尺排好测点,测点应伸入曲线两端直线范围内,将各测点顺序编号。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
3.在风力较小的条件下,用20米弦绳,在钢轨顶面作用边下16mm处,拉绳测每个测点正矢,拉弦要用力均匀,读数要眼、线、尺三者成垂线,读弦线靠钢轨一边的读数。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
4.曲中点:用测点分段数来表示的曲线中央位置为现场正矢倒累计合计除以现场正矢合计(缓和曲线不等长应抛去缓和曲线检算)。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
即:曲中点=现场正矢倒累计合计÷现场正矢合计󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(曲中点位置应按拉正矢始点方向算起,小数点后单位为米)󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
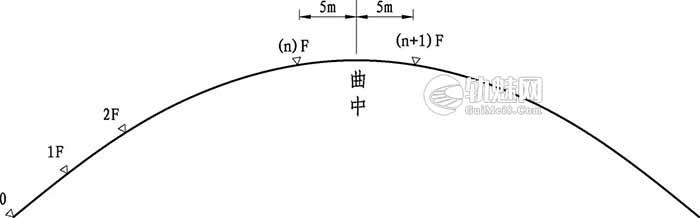
5.曲中分中布设正矢方法:
如果规整后的曲线全长减去两端缓长的长度为整10米倍数的偶数,用对桩分中法(由曲中点向两边每10米布点)。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
如果规整后的曲线全长减去两端缓长的长度为整10米倍数的奇数,用10米分中法(先由曲中点分别向两边量取5米布点,然后再向两边每10米布点),如下图:󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
二、正矢计算公式
1.圆曲线正矢:
$$f_圆=\frac{50000}{R}$$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
2.正矢递减率:
$$f_递=\frac{f_圆}{\frac{缓和曲线长}{10}}$$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
3.曲线全长:
$$L=\frac{πRα}{180}+1$$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式中α为度°,曲线偏角一般为六十进制的度°分′秒″,计算时应转化为十进制的度,l 为缓和曲线长度,如曲线两头缓和曲线不等长,应取两缓和曲线长度的平均长度。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
4.根据曲线全长算出 a、b 值,即:󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
a=(取整长度-曲线全长)÷2÷10󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
b=1-a
5.直缓点前后测点正矢:
$$f_1=\frac{b^3}{6} f_递 \\
f_2=\left (b+\frac{a^3}{6} \right ) f_递$$
6.缓圆点前后测点正矢:
$$f_{缓终}=f_圆-\left (b+\frac{a^3}{6}\right )f_d$$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$f_{圆始}=f_圆-\frac{b^3}{6}f_d$$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
7.直圆点前后测点正矢:
$$f_1=\frac{b^2}{2}×f_圆$$
$$f_2=(1-\frac{a^2}{2})×f_圆$$
三、分中法计划正矢的算例
1.无缓和曲线的单圆曲线的直、圆桩前后两点的算例:设圆曲线全长 32 米,R=4000 米,如下图:
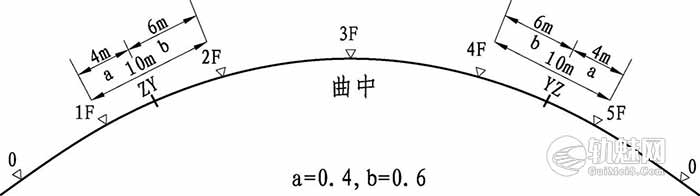
a、b 为一个表示 L 分为两段后,每段所占原长的比例系数,且 a+b=1。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$f_1=f_5=\frac{b^2}{2}×f_圆=\frac{0.6^2}{2}×\frac{50000}{4000}=2.25≈2mm$$
$$f_2=f_4=(1-\frac{a^2}{2})×f_圆=(1-\frac{0.4^2}{2})×\frac{50000}{4000}=11.5≈12mm$$
2.有缓和曲线各点正矢的算例:例:某曲线 R=600 米,缓长 50 米,如下图:󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
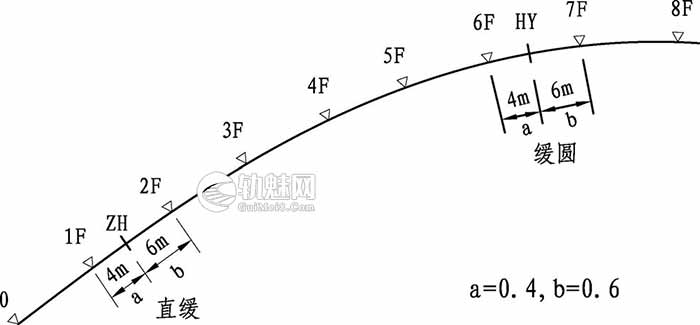
a 在外,b 在内。\(f_递=\frac{83}{5}=16.6mm\)󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
⑴直缓点前后两点正矢
$$f_1=\frac{b^3}{6} f_递=\frac{0.216}{6}× \frac{83}{5} ≈1mm$$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$f_2= (b+\frac{a^3}{6} ×f_递= (0.6+\frac{0.064}{6}× \frac{83}{5} ≈10mm$$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
⑵缓圆点前后测点的正矢
$$f_6=f_{缓终}=f_圆-\left (a+\frac{b^3}{6}\right )f_递=83-\left (0.4+\frac{0.216}{6}\right )×\frac{83}{5}≈76mm$$
$$f_7=f_{圆始}=f_圆-\frac{a^3}{6}f_递=83-\frac{0.064}{6}×16.6≈83mm$$
⑶缓和曲线各点正矢为前一点正矢加 f 递。
3.当圆曲线的曲中点位置确定后,可利用下列公式的计算通过丈量曲线上股可较精确求得缓圆点(圆缓)、󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
直缓点(缓直)位置(式中α、β单位为度):󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$圆曲线上股长度=\frac{π(R半个标准轨距半个轨头宽)(α -两端缓和曲线偏角)}{180} $$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$缓和曲线偏角β=\frac{901}{πR} $$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$缓和曲线上股长度=πβ×\frac{R+半个轨头宽}{90}$$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$HY 距曲中距离=\frac{π(R 半个标准轨距+半个轨头宽)(α -两端缓和曲线偏角)}{360} $$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$ZH 距曲中距离=\frac{π(R半个标准轨距+半个轨头宽)(α -两端缓和曲线偏角)}{360}\\+πβ×\frac{R半个标准轨距+半个轨头宽}{90}$$󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
上股缓圆点(圆缓)、直缓点(缓直)位置标定后,方至下股,缓圆点(圆缓)、直缓点(缓直)的准确󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
标定,提高机械化捣固曲线的同步点精度,从而提高机械化曲线地段的捣固质量。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
四、超高计算
超高每 5 米一点,缓和曲线各点超高,h2 点与 f1 点重合。
h1=(b×10-5)×计划超高÷缓长󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
h2~h 缓圆前点超高:hn=(b×10+5×(n-2))×计划超高÷缓长󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
h 缓圆=计划超高-a×10×计划超高÷缓长󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
无缓和曲线时,直线各点超高,h0 点与 f1 点重合,向直线方向顺坡。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
直圆点超高:
h0=计划超高
h1=h0-5×超高顺坡率
h2~hn点超高:hn=前点超高-5×超高顺坡率󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
五、利用 Excel 电子表格函数计算功能计算要点
1.曲线偏角的转化
工务技术资料中,曲线偏角单位为度分秒,个别曲线偏角的秒保留 2 位小数。Excel 的 RADIANS()函数能将角度转化为弧度,但首先要把六十进制的分秒转化为度。可以利用下式转换:󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
RADIANS((VALUE(RIGHT(TEXT(H5,”0.000000″),4))/6000+VALUE(LEFT(RIGHT(TEXT(H5,”0.000000″),6),󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
2)))/60+INT(VALUE(H5)))󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式中“H5”为曲线偏角单元格,单位为度分秒, VALUE(RIGHT(TEXT(H5,”0.000000″),4))/6000 算式是将曲线偏角的小数位增加到 6 位后,取最右边的 4 位,即取含有两位小数的秒位,除以 6000 后化为分。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
VALUE(LEFT(RIGHT(TEXT(H5,”0.000000″),6),2))算式是取分,与秒位化成分后相加除以 60 化成度,算式󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
INT(VALUE(H5))利用取整函数取度,与分除以 60 转化成的度相加,通过 RADIANS()函数将曲线偏角转化成弧度。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
2.曲线全长的计算(式中α单位为弧度)󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
根据曲线公式 R*α+(l1+l2)/2,利用 Excel 单元格间的公式计算,很方便地计算出曲线全长
3.长度向上规整
利用 CEILING()函数将小数位向上舍人的功能实现。先将长度除以 10,然后再乘以 10。,要注意的是曲线的半径通过大维修测量,给出的是线路中心的曲线半径,曲线正矢是利用钢尺在上股钢轨上测量布设,因此要计算曲线上股钢轨的长度,计算是要考虑轨距和半个轨头的影响量,如果正线曲线没有加宽,如为 P60kg钢轨,需要在原有的半径基础上加上 0.754m。确保直缓点在 1F 和 2F 之间。󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
CEILING(曲线长/10,1)*10󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
4.曲中正矢点为正点和副点的判断(正点为对桩、副点为分中)󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
利用取整后减去缓和曲线除以 10 后再除以 2,余数大于 0,为“分中”。可以利用 mod()计算两数相除的余数,利用条件函数判断“分中”或“对桩”󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
IF(MOD((O5-J5-K5)/10,2)>0,”分中”,”对桩”)󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
六、测设曲线标
根据里程标用钢尺测量并记录曲线起终里程,分别在曲线钢轨上(下)股对应新的直缓、缓圆、曲中、圆缓、缓直点的路肩上埋设、固定曲线标。
文章来源:
原文名称:曲线分中法计划正矢计算及布设方法󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
作者信息:不详
期刊信息:此文已由洛阳工务段在《郑铁工务通讯》发表󠄐󠄹󠅀󠄪󠄣󠄞󠄡󠄥󠄞󠄡󠄩󠄠󠄞󠄤󠄩󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮





感谢