普通单开道岔几何尺寸计算

以曲线半切线形尖轨、直线辙叉单开道岔为例进行道岔几何尺寸计算。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

曲线尖轨大多采用圆曲线线型。其形式很多,有切线形、半切线形、割线形、半割线形等，其中以切线形最为常用，切线形中又以半切线形尖轨最为常用。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

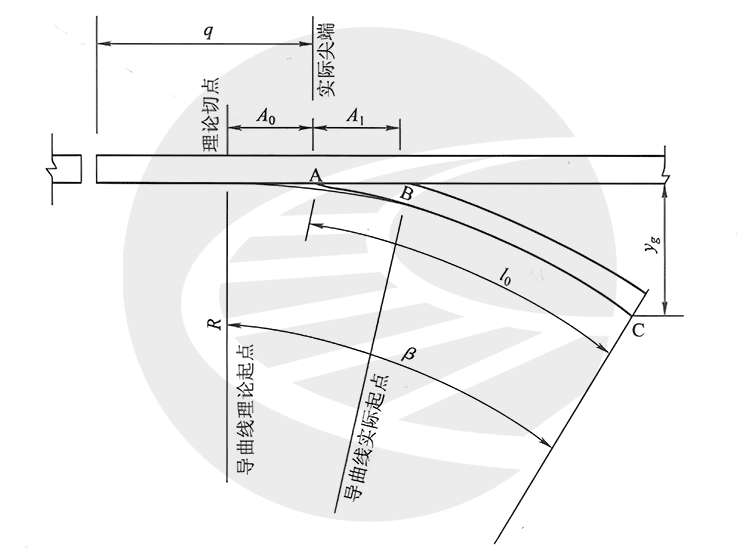
半切线形尖轨曲线的理论起点与基本轨相切,在尖轨顶宽一定宽度处(通常为20～40 mm)开始,将曲线改为切线，为避免尖轨尖端过于薄弱，在顶宽为3~5 mm处再作一斜切，如图1。这种形式的曲线尖轨的侧向行车条件较直线尖轨为好,且尖轨比较牢固,加工也比较简单,是我国目前大号道岔的标准尖轨形式。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

图1 半切线形尖轨

曲线尖轨直线辙叉单开道岔的尺寸计算原始参数包括:道岔转辙角α,曲线尖轨长l₀,直尖轨长l’₀,基本轨前端长q,导曲线半径R,尖轨转辙角β、尖轨跟端支距y_g，辙叉趾距n(辙叉理论尖端到趾端的距离)辙叉跟距m(辙叉理论尖端到跟端的距离)等。

设侧股轨道中心线的半径为R,则尖轨工作边的曲率半径R=R₀+717.5mm。曲线尖轨的长度与道岔侧线理论顶点位置.轨距递变率、跟端构造、岔枕布置等因素有关,直尖轨的尖端和跟部应与曲尖轨的尖端和跟部对齐。

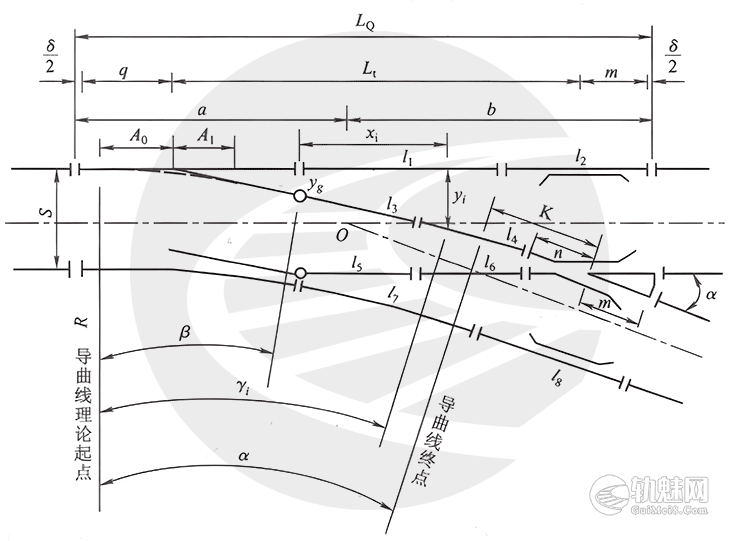
半切线形尖轨、直线辙叉单开道岔的主要尺寸如图2所示。О点为道岔直股中心线和侧股中心线的交点，又称道岔中心。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

图2 曲线尖轨直线辙叉单开道岔几何尺寸

需要计算的尺寸如下:

道岔前长α(道岔前轨缝中心到道岔中心的距离)，道岔后长b(道岔中心到道岔后端轨缝中心的距离);󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

道岔理论长L₁(尖轨实际尖端到辙叉理论尖端的距离);

道岔实际长L_Q(道岔前后轨缝中心之间的距离);

跟端之后导曲线支距。

1.道岔基本尺寸计算

由图中道岔几何关系可知,R-Rcosα+Ksinα=S则，

$$K=\frac{S-R+R\cos \alpha }{\sin \alpha }$$
$$b=\frac{S}{2\tan \frac{\alpha }{2}}+m+\frac{\delta }{2}$$
$$L_Q=q+L_t+m+\delta $$
$$\alpha =L_Q-b$$

2.道岔导曲线支距计算

在单开道岔上,自尖轨跟端起,以直股基本轨作用边为横坐标轴,导曲线外股钢轨工作边上各点距此轴的垂直距离叫做导曲线支距。导曲线支距对导曲线的圆顺起着十分重要的作用。

通常取直股基本轨作用边正对尖轨跟端处为坐标原点。令导曲线上各支距点i的横坐标为X_i,通常点间距为2m,则其相应的支距y,支距点i所对应的偏角为γ_i。

由图中几何关系知

$$R-R\cos\beta =y_g$$

则可计算出c\(\cos \beta =\frac{R-y_g}{R}\)，由三角函数可算出sinβ。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

又由于\(R\sin \gamma _i=R\sin \beta +x_i\),则可得到\(\sin \gamma _i\),进而求得\(\cos \gamma _i\)_。

则第i点的支距为

$$y_i=y_g+R(\cos \beta -\cos \gamma _i)$$

式中β——道岔转辙角。

3.配轨计算

一组单开道岔,除转辙器、辙叉及护轨外，一般有8根连接轨，分4股,每股2根。所谓配轨就是计算这8根钢轨的长度并确定接头的位置。

配轨时应考虑如下一些原则:

(1)转辙器及辙叉的左右基本轨长度,应尽可能一致,以减少基本轨备件的数量，并有利于左右开道岔的互换;󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

(2)连接部分的钢轨不宜过短,小号码道岔一般不小于4.5m,大号码道岔不小于6.25 m;󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

(3)配轨时应保证对接接头,并尽量使岔枕布置不发生困难，同时要考虑安装轨道电路绝缘接头的可能性;󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

(4)充分利用整轨、缩短轨、整轨的整分数倍的短轨，做到少锯切,少废弃,选用钢轨利用率较高的方案。
配轨计算公式如下:

$$l_1+l_2=l_Q-l_i-3\delta $$
$$l_3+l_4=(R+\frac{b}{2})(\alpha -\beta )+K-n-3\delta$$
$$l_5+l_6=l_t-l’_0-n-3\delta$$
$$l_7+l_8=R_{i\alpha }+K+m+q-A_0-2\delta -l_j$$

式中

A₀——导曲线理论起点至尖轨实际尖端的距离;

l_j———基本轨长度;

b——轨头宽度;

R_i——内轨轨头中心处导曲线半径，用下式计算:

$$R_i=(R-S-\frac{b}{2})$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

配轨计算所有公式中角度均以弧度计。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

文章来源：

 王兴强，郭兆军主编. 铁路轨道施工及维修[M]. 2014