[图解]铁路抛物线型竖曲线计算

竖曲线有圆曲线形、抛物线形和链条坡三种类型。文章源自轨魅网-https://www.guimei8.com/2142.html

对称型竖曲线

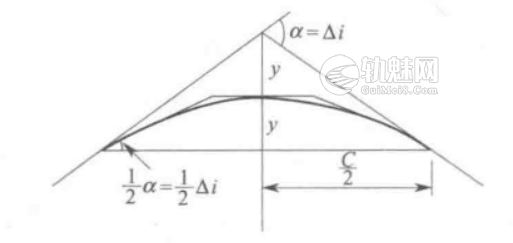
图1 抛物线型竖曲线示意

抛物线型竖曲线通常是二次抛物线，它实际上是采用以20m为边长而其变更率为γ的外切多边形所构成,其长度应该为20m的倍数,所以它的纵距可用方程式y=Ax²表示。具体参见图1。文章源自轨魅网-https://www.guimei8.com/2142.html

(1)竖曲线长度:

从图1可得文章源自轨魅网-https://www.guimei8.com/2142.html

$$\tan \frac{a}{2}=\frac{2y}{\frac{C}{2}}=\frac{1}{2}\bigtriangleup i ‰$$文章源自轨魅网-https://www.guimei8.com/2142.html

上式中C为抛物线长度,故文章源自轨魅网-https://www.guimei8.com/2142.html

$$\frac{\gamma }{\Delta i}=\frac{20}{C}$$文章源自轨魅网-https://www.guimei8.com/2142.html

又因为文章源自轨魅网-https://www.guimei8.com/2142.html

$$y=\frac{C}{8}\times \frac{\Delta i}{1000}=\frac{\Delta i\cdot C}{8000}$$文章源自轨魅网-https://www.guimei8.com/2142.html

所以,竖曲线长度C为文章源自轨魅网-https://www.guimei8.com/2142.html

$$C=\frac{\Delta i}{\gamma }\times 20\qquad（m）$$文章源自轨魅网-https://www.guimei8.com/2142.html

(2)相邻坡度代数差Δi:

$$\Delta i=\frac{\gamma \cdot C}{20}$$文章源自轨魅网-https://www.guimei8.com/2142.html

(3)每20m的变坡率γ:

$$\gamma =\frac{20\Delta i}{20}$$文章源自轨魅网-https://www.guimei8.com/2142.html

式中γ——每20m长度的变坡率(‰) ,也可由1表查得。文章源自轨魅网-https://www.guimei8.com/2142.html

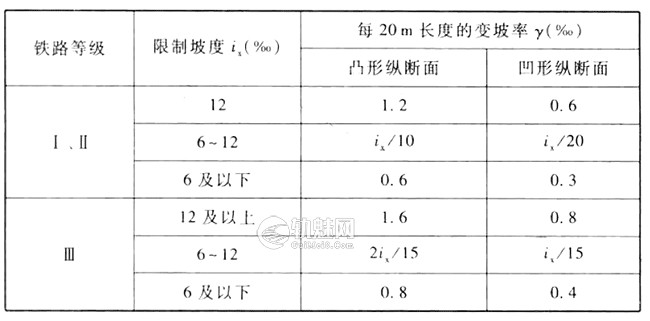
抛物线型竖曲线20m长度变坡率

(4)竖曲线切线长:

$$T=\frac{C}{2}\qquad（m）$$文章源自轨魅网-https://www.guimei8.com/2142.html

(5)竖曲线的纵距:

$$\gamma =\frac{\gamma x^2}{40000} \qquad（m）$$文章源自轨魅网-https://www.guimei8.com/2142.html

式中x——为竖曲线始、终点至任意点的距离(m)。文章源自轨魅网-https://www.guimei8.com/2142.html

(6)任意点坡度标高:

$$h=H_V\pm X\cdot i$$文章源自轨魅网-https://www.guimei8.com/2142.html

式中文章源自轨魅网-https://www.guimei8.com/2142.html

h——坡度对应点标高(m);文章源自轨魅网-https://www.guimei8.com/2142.html

X·i值——凸形用“-”,凹形用“+”;文章源自轨魅网-https://www.guimei8.com/2142.html

H_v——中央点标高(m) ;文章源自轨魅网-https://www.guimei8.com/2142.html

X——中央点至对应点的距离(m);文章源自轨魅网-https://www.guimei8.com/2142.html

i——对应点所处的坡度(‰)。文章源自轨魅网-https://www.guimei8.com/2142.html

(7)任意点竖曲线标高:

$$H=h+γ$$文章源自轨魅网-https://www.guimei8.com/2142.html

式中文章源自轨魅网-https://www.guimei8.com/2142.html

H——竖曲线对应点标高(m);文章源自轨魅网-https://www.guimei8.com/2142.html

h——坡度对应点标高(m);文章源自轨魅网-https://www.guimei8.com/2142.html

y——x对应点的纵距( mm) ,凸形用“-”,凹形用“+”。文章源自轨魅网-https://www.guimei8.com/2142.html

例题 1

已知相邻坡段之坡度如图2所示,Ⅰ级铁路,限制坡度i_x= 10‰,采用抛物线型竖曲线,其变坡点里程为K24+320,试计算竖曲线长度、切线长度及纵距和标高。文章源自轨魅网-https://www.guimei8.com/2142.html

图2 相邻坡段坡度示意

解:(1)根据题意,得变坡率:文章源自轨魅网-https://www.guimei8.com/2142.html

$$\gamma =\frac{i_x}{10}=\frac{10}{10}=1％$$文章源自轨魅网-https://www.guimei8.com/2142.html

(2)坡度代数差:文章源自轨魅网-https://www.guimei8.com/2142.html

$$\Delta i=2-(-2)=4‰$$文章源自轨魅网-https://www.guimei8.com/2142.html

(3)竖曲线长:文章源自轨魅网-https://www.guimei8.com/2142.html

$$C=\frac{\Delta i}{\gamma }\times 20=\frac{4}{1}\times 20=80m$$文章源自轨魅网-https://www.guimei8.com/2142.html

(4)切线长:文章源自轨魅网-https://www.guimei8.com/2142.html

$$T=\frac{C}{2}=\frac{80}{2}=40m$$文章源自轨魅网-https://www.guimei8.com/2142.html

(5)竖曲线始终点里程:文章源自轨魅网-https://www.guimei8.com/2142.html

始点里程A:K24+(320-40)=K24+280文章源自轨魅网-https://www.guimei8.com/2142.html

终点里程B:K24+(320+40)=K24+360文章源自轨魅网-https://www.guimei8.com/2142.html

(6)各点坡度标高:文章源自轨魅网-https://www.guimei8.com/2142.html

K24+280处:h=H_V+X_xi=120.000-40×2‰=119.920 m文章源自轨魅网-https://www.guimei8.com/2142.html

K24+300处:h=H_V+X_xi=120.000-20×2‰=119.960 m文章源自轨魅网-https://www.guimei8.com/2142.html

K24+320处:h=H_V+X_xi=120.000-0×2‰=120.000 m文章源自轨魅网-https://www.guimei8.com/2142.html

K24+340处:h=H_V+X_xi=120.000-20×2‰=119.960 m文章源自轨魅网-https://www.guimei8.com/2142.html

K24+360处:h=H_V+X_xi=120.000-40×2‰=119.920 m文章源自轨魅网-https://www.guimei8.com/2142.html

(7)各点纵距:文章源自轨魅网-https://www.guimei8.com/2142.html

$$\frac{K24+280}{K24+360}处：y=\frac{\gamma x^2}{40000}=\frac{1\times 0^2}{40000}=0.00m$$文章源自轨魅网-https://www.guimei8.com/2142.html

$$\frac{K24+300}{K24+340}处：y=\frac{\gamma x^2}{40000}=\frac{1\times 20^2}{40000}=0.01m$$文章源自轨魅网-https://www.guimei8.com/2142.html

$$K24+320处：y=\frac{\gamma x^2}{40000}=\frac{1\times 40^2}{40000}=0.04m$$文章源自轨魅网-https://www.guimei8.com/2142.html

计算结果见表2。文章源自轨魅网-https://www.guimei8.com/2142.html

表2计算结果文章源自轨魅网-https://www.guimei8.com/2142.html

例题 2

Ⅰ级线路一凹形竖曲线,i₁=-6.2‰ , i₂=+2.2‰,变坡点里程为K504+200,其标高为58.200m,如图3所示。试计算该竖曲线上每50m的设计标高。文章源自轨魅网-https://www.guimei8.com/2142.html

图3 凹形竖曲线示意

解:(1)根据题意,得坡度代数差:文章源自轨魅网-https://www.guimei8.com/2142.html

Δi=2.2-(-6.2)=8.4‰文章源自轨魅网-https://www.guimei8.com/2142.html

(2)根据题意,凹形竖曲线变坡率不得大于0.5‰ ,有短坡的变坡点数:文章源自轨魅网-https://www.guimei8.com/2142.html

$$n=\frac{\Delta i}{\gamma }=\frac{8.4}{0.5}=16.8，取整为17$$文章源自轨魅网-https://www.guimei8.com/2142.html

反算变坡率为文章源自轨魅网-https://www.guimei8.com/2142.html

$$\gamma =\frac{i_x}{n}=\frac{8.4}{17}=0.494‰$$文章源自轨魅网-https://www.guimei8.com/2142.html

(4)切线长:文章源自轨魅网-https://www.guimei8.com/2142.html

$$T=\frac{C}{2}=\frac{340}{2}=170m$$文章源自轨魅网-https://www.guimei8.com/2142.html

(5)竖曲线始终点里程:文章源自轨魅网-https://www.guimei8.com/2142.html

始点里程 K504+(200-170)= K504+030文章源自轨魅网-https://www.guimei8.com/2142.html

终点里程K504+(200+170)=K504+370(6)各点坡度标高:文章源自轨魅网-https://www.guimei8.com/2142.html

K504+030处:h=H_v+X×i₁=58.200+170×6.2‰=59.254m文章源自轨魅网-https://www.guimei8.com/2142.html

K504+050处:h=H_v+X×i₁=58.200+150×6.2‰=59.130m文章源自轨魅网-https://www.guimei8.com/2142.html

K504+100处:h=H_v+X×i₁=58.200+100×6.2‰=58.820m文章源自轨魅网-https://www.guimei8.com/2142.html

K504+150处:h=H_v+X×i₁=58.200+50×6.2‰=58.510m文章源自轨魅网-https://www.guimei8.com/2142.html

K504+250处:h=H_v+X×i₂=58.200+50×2.2‰=58.310m文章源自轨魅网-https://www.guimei8.com/2142.html

K504+300处:h=H_v+X×i₂=58.200+100×2.2‰=58.420m文章源自轨魅网-https://www.guimei8.com/2142.html

K504+350处:h=H_v+X×i₂=58.200+150×2.2‰=58.530m文章源自轨魅网-https://www.guimei8.com/2142.html

K504+370处:h=H_v+X×i₂=58.200+170×2.2‰=58.574m文章源自轨魅网-https://www.guimei8.com/2142.html

(7)各点纵距:文章源自轨魅网-https://www.guimei8.com/2142.html

$$\frac{K504+050}{K504+350}处：y=\frac{\gamma x^2}{40000}=\frac{0.0494 \times 20^2}{40000}=0.00494m$$文章源自轨魅网-https://www.guimei8.com/2142.html

$$\frac{K504+100}{K504+300}处：y=\frac{\gamma x^2}{40000}=\frac{0.0494 \times 70^2}{40000}=0.0605m$$文章源自轨魅网-https://www.guimei8.com/2142.html

$$\frac{K504+150}{K504+250}处：y=\frac{\gamma x^2}{40000}=\frac{0.0494 \times 120^2}{40000}=0.1778m$$文章源自轨魅网-https://www.guimei8.com/2142.html

$$K504+200处：y=\frac{\gamma x^2}{40000}=\frac{0.0494 \times 170^2}{40000}=0.3569m$$文章源自轨魅网-https://www.guimei8.com/2142.html

(8)各点竖曲线标高:文章源自轨魅网-https://www.guimei8.com/2142.html

K504+300处:H=h+y=58.420+0.0605=58.481m文章源自轨魅网-https://www.guimei8.com/2142.html

K504+350处:H=h+y=58.530+0.0049=58.535m文章源自轨魅网-https://www.guimei8.com/2142.html

K504+370处:H=h+y=58.574+0=58.574m文章源自轨魅网-https://www.guimei8.com/2142.html

K504+030处:H=h+y=59.254+0=59.254m文章源自轨魅网-https://www.guimei8.com/2142.html

K504+050处:H=h+y=59.130+0.0049=59.135m文章源自轨魅网-https://www.guimei8.com/2142.html

K504+100处:H=h+y=58.820+0.0605=58.881m文章源自轨魅网-https://www.guimei8.com/2142.html

K504+150处:H=h+y=58.510+0.1778=58.688m文章源自轨魅网-https://www.guimei8.com/2142.html

K504+200处:H=h+y=58.200+0.3569=58.557m文章源自轨魅网-https://www.guimei8.com/2142.html

K504+250处:H=h+y=58.310+0.1778=58.488m文章源自轨魅网-https://www.guimei8.com/2142.html

计算结果见表3。文章源自轨魅网-https://www.guimei8.com/2142.html

本例题也可直接运用变坡率γ=0.5‰ ,计算结果相差无几。在这里只是多介绍一种方法。文章源自轨魅网-https://www.guimei8.com/2142.html

文章来源：

陈知辉编著. 《铁路曲线轨道》[M]. 2009文章源自轨魅网-https://www.guimei8.com/2142.html