由于轮轨滚动接触,钢轨轨头踏面容易产生疲劳损伤,严重危害钢轨的使用寿命。在役钢轨轨头踏面常见斜裂纹形貌如图1所示。由图1可见:轨头踏面裂纹一般分布在工作边的轨距角侧。萌生初期的表面裂纹普遍与钢轨顶面呈约10°~40°的夹角,其中部分裂纹向钢轨内部扩展,并改向成水平走向或沿表面扩展形成剥离掉块;另一部分裂纹沿轨面向下扩展,会突然以较大角度约60°~70°向内部深处和横向扩展,导致钢轨横向断裂[1-4]。通过研究钢轨表面裂纹深度的定量评估方法以判定裂纹的严重程度,对后续处理措施的选择具有重要意义,并可实现钢轨伤损的早期预警。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

图1 钢轨踏面斜裂纹内部纵向剖面图
对在役钢轨采用人工目视进行伤损检查,很容易产生漏检,且无法判定钢轨裂纹的严重程度。采用磁粉、渗透等常规无损检测方法进行钢轨探伤时,不但会造成污染,而且检测效率都比较低,需要进行表面预处理以及一定的光照条件,尤其是渗透检测只能检测已开口的表面缺陷。王平等[5]研究了钢轨表面缺陷的漏磁三维磁场分析,采用三维磁场测量以及有限元方法对缺陷漏磁场的三维分布情况进行了分析;王凌云等[6]研究了重轨表面缺陷机器视觉检测的关键技术,包括缺陷的红外成像处理、多CCD组合采集、缺陷提取等;刘洋等[7]根据激光超声波在钢轨表面激发时会同时产生纵波、横波和表面波,而表面波可用于检测表面微裂纹的原理,研究了激光超声技术在钢轨探伤中的应用。
以上将漏磁、红外和激光超声等检测技术应用于钢轨,在目前还仅限于实验室研究,未见现场实用的报道;另外,这3种检测方法虽然不需要耦合剂即可实现非接触检测,但是,漏磁检测方法需要保证探头与检测面的间隙恒定,否则漏磁场变化很大,且漏磁检测方法还需要对钢轨进行磁化,然而磁化设备较笨重;红外检测设备成本高,而且无法实现缺陷深度的评估;激光超声检测方法目前主要应用于高温状态下的远距离检测,属于微损检测,需要的设备功率大,且设备寿命短、成本也较高。目前,中国铁道科学研究院在钢轨探伤车原有超声检测技术的基础上,研究增加脉冲涡流技术用于检测钢轨表面裂纹,但是也仅限于试验阶段。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
涡流检测作为常规的无损检测方法之一,其检测原理是当涡流检测线圈通入交变电流时,线圈周围就会产生交变磁场,将金属导体置于该交变磁场中,金属导体的表面就会感应出涡流,而此涡流又会产生1个磁场,该磁场与原线圈磁场相互作用,阻碍原磁场的变化。当金属导体的表面或近表面有缺陷时,就会引起涡流的畸变,使感应的涡流发生变化,导致检测线圈的阻抗或电压发生变化,分析该电压或阻抗的变化就可以实现对金属导体表面和近表面的缺陷检测。由于在役钢轨的检测只能在“天窗点”进行,而且是夜间作业,时间紧,光照条件有限,因此,具有非接触、无污染、不需要耦合剂、检测速度快等特点的涡流检测方法适宜用于在役钢轨表面缺陷的检测。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
本文首先通过仿真计算,拟合钢轨表面裂纹深度与磁感应强度之间的函数关系。然后按照该函数关系得到钢轨表面裂纹深度与涡流检测信号电压幅值的关系式,实现对在役钢轨表面裂纹的有效检测及深度的定量评估。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
1 钢轨表面裂纹涡流检测的定量仿真
根据涡流检测原理,被测导体中感应的涡流密度为
$$J(Z)=J_0(Z)exp\left ( -Z/\sqrt{\frac{2}{\omega \mu \sigma }}\right ) \quad(1)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
其中,\(\omega=2\pi f\)󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式中:J为涡流密度;Z为距离导体表面的距离;J0为面电流密度;ω 和f 分别为涡流激励信号的角频率和频率;μ和σ 分别为被测导体的磁导率和电导率。
涡流渗透深度为
$$\delta =\frac{1}{\sqrt{\omega \mu \sigma }} \quad(2)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式中:δ为涡流渗透深度。
由式(1)和式(2)可见:被测导体表面的涡流密度随着检测深度的增加成指数衰减,但随着频率、电导率和磁导率的增大而增大;虽然频率、电导率和磁导率越大,导体表面涡流的密度也越大,但是涡流的趋肤效应也越显著、渗透深度也越小;由于趋肤效应,涡流检测只能实现被测导体表面或近表面深度的缺陷检测。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
1.1 涡流检测钢轨表面裂纹深度的定量仿真分析
采用ANSYS软件,以1块表面带有裂纹的钢板模拟钢轨,建立涡流检测模型,进行钢轨表面裂纹涡流检测响应的仿真计算分析。该模型主要由含有裂纹的钢板、涡流线圈(绝对式)和空气组成。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
由于涡流渗透深度的限制,且钢轨的长、宽尺寸与涡流线圈直径比大于5、钢轨厚度与涡流渗透深度比例大于4,则可认为钢轨对线圈阻抗的影响与其无限长时一致。在钢板中心刻有槽形裂纹,将线圈置于钢板中心线上,从左至右逐点扫查,如图2所示。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

图2 模型及线圈扫查示意图
线圈模型耦合至外接电路,仿真时裂纹长×宽为9.0 mm×0.2 mm、深度分别为0.1,0.2,0.5,1.0,1.5,2.0和5.0mm。仿真模型中线圈和钢板的几何尺寸及材料性能参数见表1。钢轨属于铁磁性材料,其相对磁导率远大于1;由于实际检测在不施加磁化的条件下进行,而线圈产生的交变磁场导致钢板的磁滞效应也非常微弱,因此可将钢板相对磁导率设为定值。
仿真模型中,裂纹附近的网格按等比例划分,其余部分使用不大于1/3的过渡尺寸网格进行划分,如图3所示。钢板整体模型的外围覆盖了其尺寸5倍的空气层以及10倍的远场空气层,模拟电磁场在无限远处的耗散问题。线圈通过场—路耦合供电。当线圈处于裂纹正上方时,钢板具有对称的涡流分布,因此求解计算完成后,当线圈处于裂纹正上方时,提取钢板中心线-4~4mm (以裂纹中心为原点)范围内的磁感应强度。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
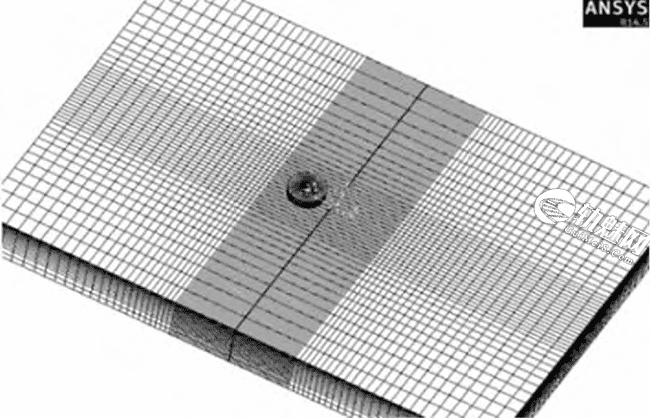
图3 钢板和线圈有限元模型
1.2 仿真结果分析
钢板中心线上不同深度裂纹对应的磁感应强度分布曲线如图4所示。从图4可以看出:磁感应强度在缺陷附近出现“双肩”现象;当裂纹深度变化时,“双肩”现象处由涡流变化导致的磁感应强度变化也较大;当裂纹深度较浅时,裂纹附近磁感应强度较大,随着裂纹深度的逐渐加大,磁感应强度逐渐变小,且变化速率逐渐减缓。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
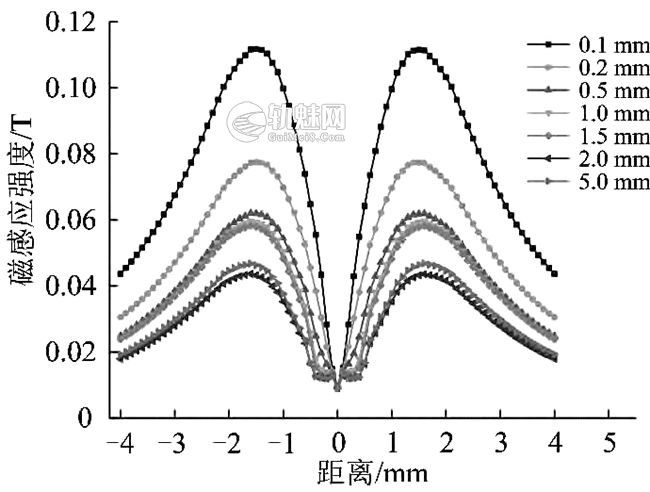
图4 钢板中心线上的磁感应强度曲线
取距裂纹中心0~0.6mm 范围内、间隔为0.1mm的点,得到这些不同位置处不同裂纹深度对应磁感应强度的变化关系,如图5所示。从图5可以看出:随着裂纹深度的加深,磁感应强度逐渐减小;当裂纹深度大于2mm时,磁感应强度几乎看不出变化。
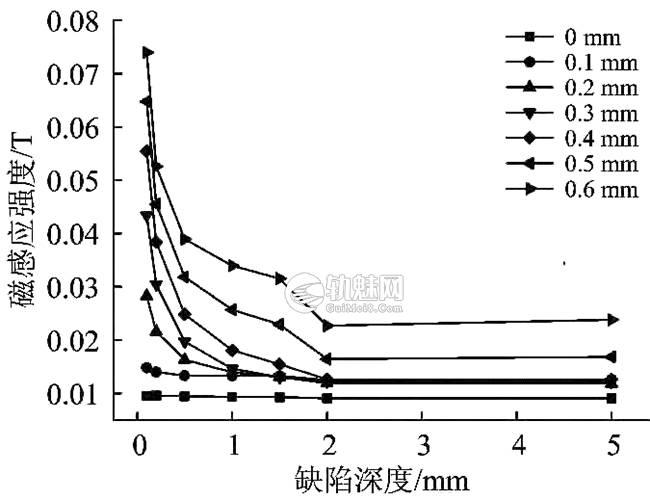
图5 距裂纹中心不同位置处裂纹深度与磁感应强度的变
其中,距裂纹中心0.3mm处裂纹深度与磁感应强度的对应关系如图6所示。从图6可以看出:随着裂纹深度的加深磁感应强度减小,当裂纹深度约为2mm以上时磁感应强度变化越来越不明显;且该深度值随着激励信号频率的变化而改变;从图中拟合曲线可以看出磁感应强度与裂纹深度近似服从指数关系。

图6 距裂纹中心0.3mm处裂纹深度与磁感应强度-深度的对应关系
从以上仿真结果可以得出:裂纹深度越深,钢板表面的磁感应强度变化越小;当裂纹深度增加到一定程度(大约2mm)后,裂纹深度再增加时的磁感应强度几乎没有什么变化。从仿真结果可以推断,当裂纹深度达到一定程度后,定量评估的误差也会越来越大。
2 钢轨试块表面裂纹涡流检测的定量评估试验
一般地,涡流检测结果只能进行定性判定,无法真正实现定量评估。目前主要采用当量法,以人工缺陷的当量表征缺陷的大小,这需要制作尽可能多的对比试块。由于采用的人工试块有限,通过当量法实现定量分析会存在很大的误差,难以得到较为准确的结果。
根据试验测试得到的不同表面裂纹深度所对应的涡流检测信号电压幅值,结合上文仿真分析的结果,按照指数函数拟合相关度较高的表面裂纹深度与涡流检测信号电压幅值的关系式,据此计算裂纹深度,可减小完全依赖试块进行定量评估所带来的误差,适用于在役钢轨检测过程中裂纹深度的快速定量评估。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
制作表面带有不同倾角、不同深度垂直裂纹和斜裂纹的钢轨试块,带有垂直裂纹钢轨试块上的裂纹深度分别取为0.5,1.0,2.0和5.0mm;带有斜裂纹钢轨试块的等效垂直深度分别取为1.0和2.0mm,斜裂纹与踏面的夹角即倾角分别为15°,30°,45°和60°,斜裂纹的等效垂直深度根据三角函数关系计算得到。图7所示为等效垂直深度为2mm、带有不同倾角的斜裂纹钢轨试块。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

图7 斜裂纹试块图(单位:mm)
利用涡流笔式探头对上述试块进行检测试验,试验过程中尽量使线圈的提离高度一致,目的是去除由于提离高度不一致对检测结果的影响,并保持检测频率和增益不变。检测步骤如下。
(1)先标定对比试块,这里假定以0.5mm深的裂纹作为判废标准,设定报警阈值。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(2)使仪器设置的增益和检测频率不变,并记录。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(3)检测上述3种不同的试块,记录涡流检测信号等效电压的幅值和相位,每个裂纹重复检测3次并记录,得到的检测数据见表2。然后根据检测数据制作等效电压幅值与裂纹深度的对应关系图;󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
根据关系图按指数曲线函数进行拟合。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
由检测数据得到的裂纹深度与等效电压幅值关系如图8所示。从图8可以看出:裂纹的深度和涡流信号等效电压幅值成一定的关系;随着裂纹深度的加深,幅值呈上升趋势,但裂纹深度增加到一定的值时,其幅值增加的速度趋缓。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
将检测数据按下式进行拟合。
表2 对比试块裂纹深度与涡流检测信号等效电压幅值的关系󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
| 序号 | 裂纹等效垂直深度/mm | 裂纹长度/mm | 裂纹倾角/(°) | 涡流检测信号等效电压 | |||
| 幅值1 | 幅值 2 |
幅值 3 |
均值 | ||||
| 1 | 0.5 | 0 5 | 90 | 39 | 41 | 34 | 41 |
| 2 | 1.0 | 1.0 | 90 | 50 | 54 | 51 | 51 |
| 3 | 2.0 | 2.0 | 90 | 73 | 70 | 74 | 73 |
| 4 | 5.0 | 5.0 | 90 | 107 | 102 | 103 | 103 |
| 5 | 1.0 | 3.9 | 15 | 85 | 88 | 91 | 88 |
| 6 | 1.0 | 2.0 | 30 | 69 | 72 | 75 | 72 |
| 7 | 1.0 | 1.4 | 45 | 63 | 64 | 62 | 63 |
| 8 | 1.0 | 1.2 | 60 | 57 | 57 | 58 | 57 |
| 9 | 2.0 | 7.7 | 15 | 107 | 105 | 108 | 107 |
| 10 | 2.0 | 4.0 | 30 | 92 | 100 | 100 | 100 |
| 11 | 2.0 | 2.8 | 45 | 84 | 85 | 92 | 85 |
| 12 | 2.0 | 2.3 | 60 | 80 | 83 | 85 | 83 |
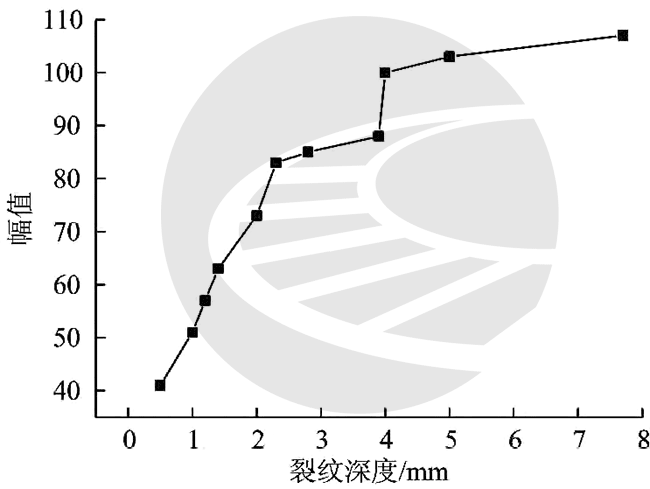
图8 裂纹深度与涡流检测信号等效电压幅值的关系曲线
$$y=y_0+A_1e^{-\frac{x}{t}} \quad(3)$$
式中:x为裂纹深度;y为涡流检测信号等效电压幅值;y0和A1和t均为需要求解的系数。
利用表2中的检测数据,求解式(3)中的未知系数,得到的拟合曲线如图9所示,拟合公式为󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$y=111.07-88.19e^{-\frac{x}{2.287}} \quad(4)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
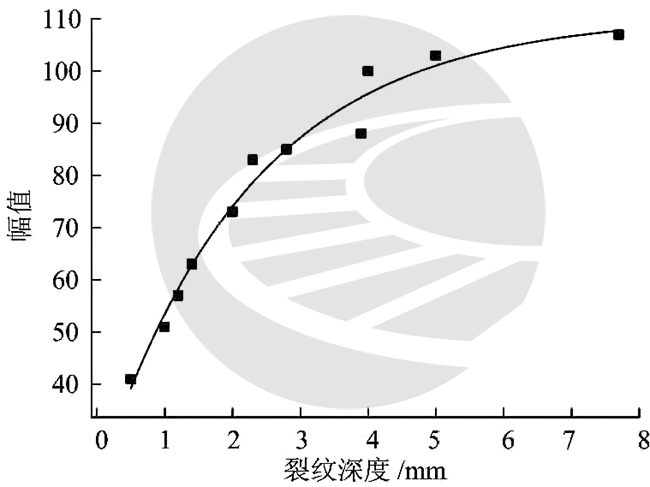
图9 指数拟合曲线
计算拟合曲线与真实数据之间的相关系数为0.975。从图9可以看出:涡流检测信号的等效电压幅值随着裂纹深度的增加逐渐增大,但随着深度增加到一定值后,幅值增大的速度趋缓。
根据拟合曲线,可通过计算机软件程序实现裂纹深度的自动计算。需要注意的是如果更换探头,需要重新取数据,并重新计算指数拟合曲线,因探头的灵敏度参数会有差异,一般将探头以工艺参数的形式设定好后就不需要改动了。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
3 钢轨表面自然裂纹的试验研究
截取一表面带自然裂纹的钢轨轨头进行检测试验,计算自然裂纹的深度。取5处裂纹做好标记,然后进行涡流检测试验,得到涡流检测信号的等效电压幅值y,将y 代入式(4),得到钢轨裂纹深度x 的结果见表3。
将上述钢轨轨头处进行纵向解剖截取,在截面上用着色方法进行检测,测量标记处的斜裂纹长度,结果见表3,裂纹着色显示如图10所示,金相显微图像如图11所示。从图上清晰可见表面斜裂纹显示。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
表3 斜裂纹的定量计算深度及其与实测深度的误差󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
| 编号 | 涡流信号等 效电压幅值 |
斜裂纹计算 深度/mm |
斜裂纹实测 深度/mm |
相对 误差/% |
| 1 | 75 | 1.718 | 1.6 | 6.9 |
| 2 | 87 | 2.996 | 2.7 | 9.9 |
| 3 | 94 | 3.793 | 3.3 | 10.5 |
| 4 | 100 | 4.772 | 4.0 | 16.2 |
| 5 | 105 | 6.148 | 5.0 | 18.7 |
从表3可以看出:实际测量的裂纹深度和检测计算得到的裂纹深度存在一定的误差,随着裂纹深度加深,检测误差会变大。其主要原因是:①试块裂纹制作精度存在一定误差,特别是深裂纹的误差更大,深度越深,其裂纹宽度越难控制;②裂纹深度通过拟合曲线计算得到,拟合曲线只能无限逼近真实值,不等于真实值;③裂纹深度达到一定深度后,感应的涡流密度迅速衰减,且裂纹倾斜向下而涡流探头的检测面积有限,给定量工作造成更大的难度。
- 图10 钢轨表面裂纹纵向解剖渗透检测图
- 图11 金相显示图
4 结论
(1)通过仿真计算,求解具有高相关系数的涡流检测信号幅值与裂纹深度的指数拟合曲线。仿真计算表明:随着裂纹深度的加深磁感应强度增大,但随着深度加深,当裂纹深度在约2mm以上时,磁感应强度的变化越来越不明显,该深度值随着激励信号频率的变化而改变,磁感应强度与裂纹深度近似服从指数关系。
(2)通过制作不同倾斜角度和深度的裂纹对比试块,采用涡流检测方法对其进行裂纹深度定量分析研究,以实现钢轨表面自然裂纹深度的定量评估。试验结果表明:裂纹深度越深,定量评估的误差越大;当裂纹深度大于2mm时定量评估误差将大于10%,当裂纹深度超过5mm时,建议结合超声检测的方法进行深度定量评估。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(3)涡流检测方法能实现钢轨表面裂纹的有效检测,并实现裂纹深度的定量评估。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
文章来源:
原文名称:钢轨表面裂纹涡流检测定量评估方法󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
作者信息:黄凤英(中国铁道科学研究院金属及化学研究所,北京 100081)󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
期刊信息:《中国铁道科学》2017年第2期󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮





