铁路曲线加宽的确定原则及计算公式

机车车辆进人曲线轨道时,仍然存在保持其原有行驶方向的惯性,只是受到外轨的引导作用方才沿着曲线轨道行驶。在小半径曲线,为使机车车辆顺利通过曲线而不致被楔住或挤开轨道,减小轮轨间的横向作用力,以减少轮轨磨耗,轨距要适当加宽。加宽轨距,系将曲线轨道内轨向曲线中心方向移动,曲线外轨的位置则保持与轨道中心半个轨距的距离不变。曲线轨距的加宽值与机车车辆转向架在曲线上的几何位置有关。

一、曲线轨距加宽的目的和方法

行驶中的机车车辆进人曲线轨道时,由于惯性作用仍然力图保持其原来的行驶方向,只有受到外轨的导向作用后才会沿曲线轨道行驶。为使机车车辆能顺利通过曲线,并使轮轨间的横向作用力最小，减少轮轨磨耗,在半径很小的曲线轨道上,轨距要适当加宽。加宽轨距,是将曲线轨道内轨向曲线中心方向移动,曲线外轨的位置则保持不变。

轨距加宽必须满足一定的条件,并受到一定的限制。在我国的轨道和机车车辆条件下,曲线轨道上能切实保证车轮不掉道的最大轨距可达1450mm,即加宽15mm。但是,超过必要的轨距加宽值会使列车通过时作用于钢轨上的横向水平力增加。因此,曲线轨道的轨距加宽必须加以严格控制。

由于列车中车辆占极大多数,所以确定曲线轨道轨距加宽标准时,应以主要类型的车辆能顺利通过为计算依据。对蒸汽机车和少量特殊形式的车辆，仅在必要时才检算其所需要的轨距。

二、转向架的内接形式

由于轮轨游间的存在.机车车辆的车架或转向架通过曲线轨道时,可以占有不同的几何位置,即可以有不同的内接形式。随着轨距大小的不同,机车车辆在曲线上可呈现以下四种内接形式。

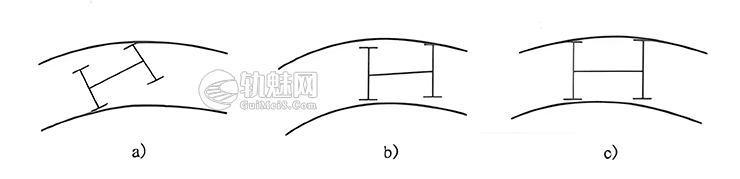
(1)斜接

机车车辆车架或转向架外侧最前位车轮轮缘与外轨作用边接触,内侧最后位车轮轮缘与内轨作用边接触,如图a)所示。

(2)自由内接

机车车辆车架或转向架外侧最前位车轮轮缘与外轨作用边接触,其他各轮轮缘无接触地在轨道上自由行驶,如图b)所示。

(3)楔形内接

机车车辆车架或转向架外侧最前位和最后位车轮轮缘同时与外轨作用边接触,内侧中间车轮(轴为奇数时)或最靠近中间的两车轮(轴为偶数时)轮缘与内侧轨距线接触,如图c)所示。

(4)正常强制内接通过
为避免机车车辆以斜接形式通过曲线,对楔形内接所需轨距增加ρ_min/2,此时转向架在曲线上所处位置称为正常强制内接。

三、轨距加宽的确定原则

机车车辆车架或转向架通过曲线轨道时,所占有的位置由轮轨间相互作用力的平衡条件和游间大小而定。应当指出,机车车辆以斜接条件通过曲线轨道时,会引起过大的蛇行运动，而以楔接条件通过曲线轨道时,又会增加列车的行车阻力和钢轨的侧面磨耗,因而都是不可取的。毫无疑问,自由内接是机车车辆通过曲线轨道的最有利方式,但机车和车辆的固定轴距长短不一,不能全部满足自由内接通过。为此，确定轨距加宽必须满足如下原则。

(1)保证占列车大多数的车辆能以自由内接形式通过曲线。

(2)保证固定轴距较长的机车通过曲线时,不出现楔形内接,但允许以正常强制内接形式通过。

(3)保证车轮不掉道,即最大轨距不超过容许限度。

四、计算公式

1.根据车辆条件确定轨距加宽

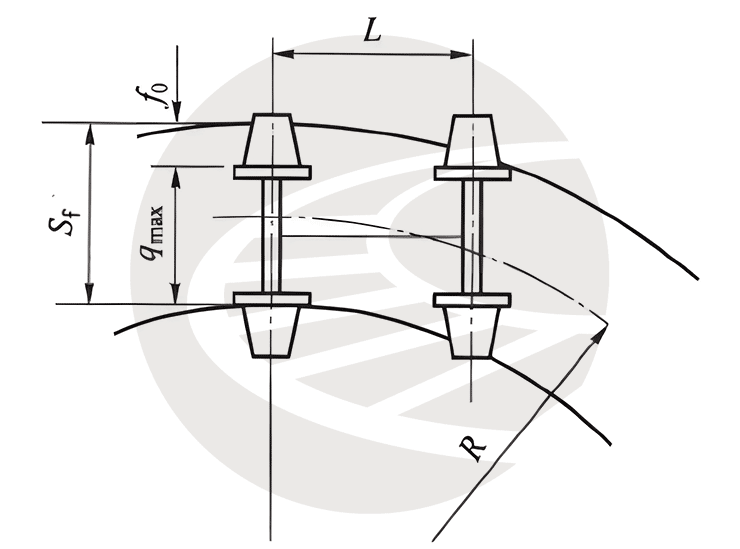
我国绝大部分的车辆转向架是两轴转向架。当两轴转向架以自由内接形式通过曲线时,前轴外轮轮缘与
外轨的作用边接触,后轴占据曲线垂直半径的位置,如图所示。则自由内接形式所需最小轨距为:

$$S_f=q_{max}+f_0$$

式中:

S_f——自由内接所需轨距(mm);

q_max——最大轮对宽度(mm),见表1;

f₀——外矢距,其值为:\(f_0=\frac{L^2}{2R}\),其中,L为转向架固定轴距(mm),R为曲线半径(mm)。

若用S₀表示直线轨道轨距,则曲线轨道轨距加宽e应为:

$$e=S_f-S_0$$

现以我国目前主型客车“202″型转向架为例计算如下:

设：     R=350m,L=2.4 m,q_max=1424 mm

则：\(f_0=\frac{L^2}{2R}=\frac{\left (2.4\times 1000 \right )^2}{2\times350\times1000}=8.2mm\)

S_f=q_max+f₀=1424+8=1432(mm)

曲线轨道轨距不应小于直线轨道轨距。由以上计算可知,对曲线半径为350m及以上的曲线轨道,轨距仍应采用1435mm,无需加宽。

2.根据机车条件检算轨距加宽

在行驶的列车中，机车数量要比车辆少得多,因此允许机车按较自由内接所需轨距为小的“正常强制内接”通过曲线。

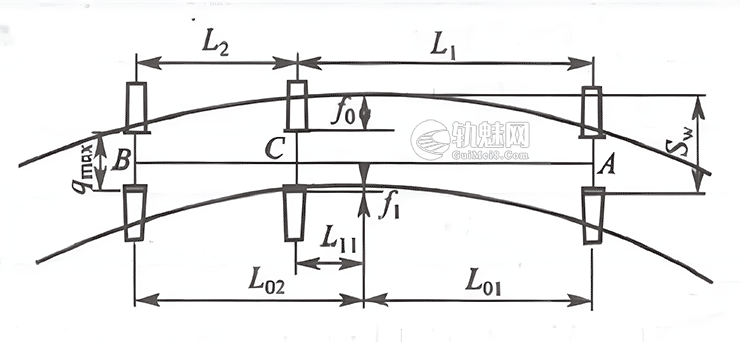
曲线轨距加宽计算图

如上图所示为一个车辆没有横动量的三轴机车车架,在轨道中处于楔形内接状态。

车架处于楔形内接时所需要的最小轨距S_w为:

$$S_w=q_{max}+f_0-f_i$$

式中:

q_max——最大轮对宽度;

f₀——前后两端车轴外轮在外轨作用边上形成的矢距，其值为:\(f_0=\frac{L^2_{01}}{2R}\),其中，\(L_{01}=\frac{L_1+L_2}{2}\),L₁为第一轴至第二轴距离,L₂为第二轴至第三轴距离;

f₁——中间轴内轮在内轨作用边上形成的矢距,其值为:\(f_1=\frac{L^2_{11}}{2R}\),其中,L₁₁为第二轴至与车架纵轴垂直的曲线半径之间的距离,其值为:L₁₁= L₀₂ – L₂。

为了保证机车以正常强制内接方式通过曲线轨道,轮轨游间至少应有相当于直线轨道上最小游间的半数。由此得所需要的轨距\(S’_w\)为:

$${S}’_\omega =S_\omega+\frac{\delta _{min}}{2}=q_{max}+f_0-f_1+\frac{\delta _{min}}{2}$$

式中:δ_min——直线轨道轮轨间的最小游间。

五、曲线轨道的最大允许轨距

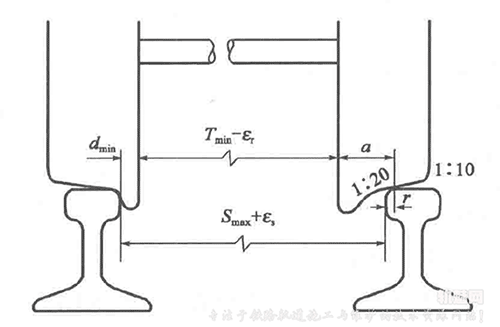
曲线轨道的最大轨距,应切实保障行车安全,不使机车车辆掉道。在最不利情况下，当轮对的一个车轮轮缘紧贴一股钢轨时,另一个车轮踏面的1:10斜坡段部分,应全部在轨头顶面范围内滚动,如上图所示。

图中

d_min——车辆车轮最小轮缘厚度,其值为22 mm;

T_min——车轮最小轮背内侧距离;

ε_r——车辆车轴弯曲时轮背内侧距离缩小量,取2mm;

a——轮背至踏面斜度为1:20与1 :10变坡点的距离,取100 mm;

r——钢轨顶面圆角宽度,取12 mm;

ε_s——钢轨弹性挤开量,取2 mm。

由此，曲线上容许最大轨距S_max由下式计算: .

$$S_{max}=d_{min}+T_{min}-\varepsilon _r+a-r -\varepsilon _s$$

将上述采用的数据代人得:S_max= 22+1350-2+100-12-2=1456( mm)

对于v_max≤120km/h的线路,其轨距的容许偏差不得超过6mm,所以曲线轨道最大容许轨距应为1 450mm,即最大允许加宽15mm。

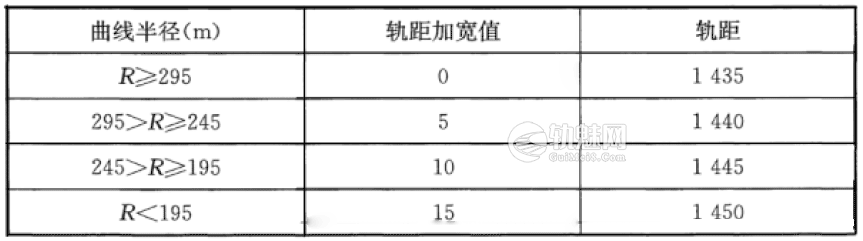
《铁路轨道设计规范》(TB10082-2017)规定:新建、改建及线路大修或成段更换轨枕地段,应按下表规定的标推进行曲线轨距加宽,未按该标准调整前的线路可维持原标准。曲线轨距加宽递减率一般不得大于1‰,特殊条件下,不得大于2‰。

文章来源：

《轨道工程》（杨荣山 著作）2013版